题目内容
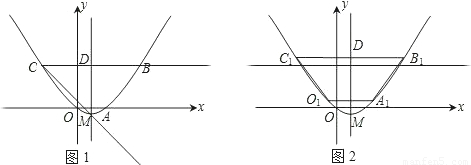
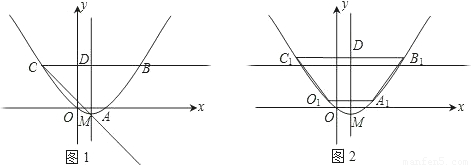
如图1,已知梯形OABC,抛物线分别过点O(0,0)、A(2,0)、B(6,3).
(1)直接写出抛物线的对称轴、解析式及顶点M的坐标;
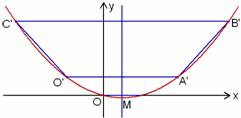
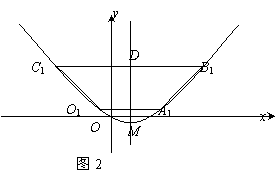
(2)将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移,分别交抛物线于点O1、A1、C1、B1,得到如图2的梯形O1A1B1C1.设梯形O1A1B1C1的面积为S,A1、 B1的坐标分别为 (x1,y1)、(x2,y2).用含S的代数式表示x2-x1,并求出当S=36时点A1的坐标;
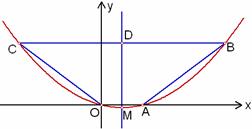
(3)在图1中,设点D的坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似?若存在,请求出t的值;若不存在,请说明理由.
(1)抛物线的对称轴为直线![]() ,解析式为
,解析式为![]() ,顶点为M(1,
,顶点为M(1,![]() ).
).
(2) 梯形O1A1B1C1的面积![]() ,由此得到
,由此得到![]() .由于
.由于![]() ,所以
,所以![]() .整理,得
.整理,得![]() .因此得到
.因此得到![]() .
.
当S=36时,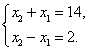 解得
解得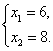 此时点A1的坐标为(6,3).
此时点A1的坐标为(6,3).
(3)设直线AB与PQ交于点G,直线AB与抛物线的对称轴交于点E,直线PQ与x轴交于点F,那么要探求相似的△GAF与△GQE,有一个公共角∠G.
在△GEQ中,∠GEQ是直线AB与抛物线对称轴的夹角,为定值.
在△GAF中,∠GAF是直线AB与x轴的夹角,也为定值,而且∠GEQ≠∠GAF.
因此只存在∠GQE=∠GAF的可能,△GQE∽△GAF.这时∠GAF=∠GQE=∠PQD.
由于![]() ,
,![]() ,所以
,所以![]() .解得
.解得![]() .
.
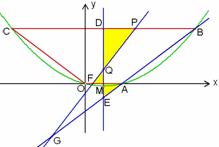
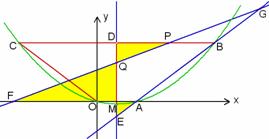
图3 图4

 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案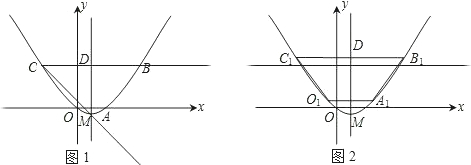
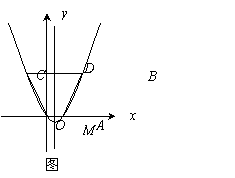 (3)在图1中,设点D坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、
(3)在图1中,设点D坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、