题目内容
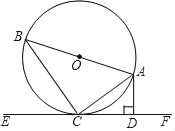
【题目】已知:如图AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
(1)求证:∠BAC=∠CAD;
(2)若∠B=30°,AB=12,求AC的长.
【答案】(1)见解析 (2)6
【解析】试题分析:(1)连接OC,利用切线和半径OA=OB构成的等腰三角形可以得到∠BAC=∠CAD;(2) 特殊直角三角形,30°对应的边是斜边一半.
试题解析:
(1)证明:连接OC,如图,
∵DE为切线,
∴OC⊥DE,
而AD⊥EF,
∴OC∥AD,
∴∠OCA=∠CAD,
∵OA=OC,
∴∠BAC=∠OCA,
∴∠BAC=∠CAD;
(2)解:∵AB为直径,
∴∠ACB=90°,
在Rt△ABC中,∵∠B=30°,
∴AC=![]() AB=
AB=![]() ×12=6.
×12=6.


练习册系列答案
相关题目
【题目】小明上周零花钱使用情况:(规定:超过50元记为正,少于50元记为负)
星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
+11 | +10 | ﹣17 | +18 | ﹣12 |
请你解答以下问题:
(1)上星期五小明用了多少零花钱;
(2)上星期四比上星期三多花了多少零花钱;
(3)求上周平均每天用多少钱?