题目内容
已知实数x，y满足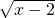
+（y+1）2=0，则xy等于
- A.3
- B.-
- C.1
- D.
D
分析：根据非负数的性质列式求出x、y的值，然后根据负整数指数次幂等于正整数指数次幂的倒数进行计算即可得解．
解答：根据题意得，x-2=0，y+1=0，
解得x=2，y=-1，
所以，xy=2-1=．
故选D．
点评：本题考查了负整数指数次幂等于正整数指数次幂的倒数的性质，非负数的性质，根据几个非负数的和为0时，这几个非负数都为0求出x、y的值是解题的关键．
分析：根据非负数的性质列式求出x、y的值，然后根据负整数指数次幂等于正整数指数次幂的倒数进行计算即可得解．
解答：根据题意得，x-2=0，y+1=0，
解得x=2，y=-1，
所以，xy=2-1=
．故选D．
点评：本题考查了负整数指数次幂等于正整数指数次幂的倒数的性质，非负数的性质，根据几个非负数的和为0时，这几个非负数都为0求出x、y的值是解题的关键．
练习册系列答案
相关题目
已知实数a、b满足a＜b，则下列式子中正确的是（ ）
A、
| ||||
| B、b-a＞0 | ||||
| C、a2＜b2 | ||||
| D、a4＜b4 |