Question

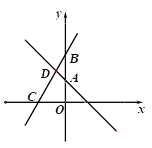
【题目】在平面直角坐标系中直线y=x+2与反比例函数 y=﹣ 的图象有唯一公共点，若直线y=x+m与反比例函数y=﹣ 的图象有2个公共点，则m的取值范围是（ ）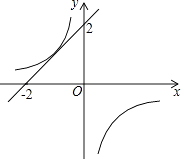
A.m＞2
B.﹣2＜m＜2
C.m＜﹣2
D.m＞2或m＜﹣2

Answer 1

【答案】D
【解析】解：根据反比例函数的对称性可知：直线y=x﹣2与反比例函数y=﹣ 的图象有唯一公共点， ∴当直线y=x+m在直线y=x+2的上方或直线y=x+m在直线y=x﹣2的下方时，直线y=x+m与反比例函数y=﹣ 的图象有2个公共点，
∴m＞2或m＜﹣2．
故选D．
根据反比例函数的对称性即可得知：直线y=x﹣2与反比例函数y=﹣ 的图象有唯一公共点，结合函数图象即可得出当直线y=x+m在直线y=x+2的上方或直线y=x+m在直线y=x﹣2的下方时，直线y=x+m与反比例函数y=﹣ 的图象有2个公共点，由此即可得出m的取值范围．