题目内容
如图,在等腰梯形ABCD中,AB∥DC,AB=9cm,CD=3cm,AD=6cm.点P从点A出发,以2cm/s的速度沿AB向终点B运动;点Q从点C出发,以1cm/s的速度沿CD向终点D运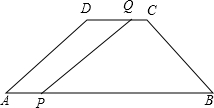 动(P、Q两点中,有一个点运动到终点时,所有运动即终止),设P、Q同时出发并运动了t秒.
动(P、Q两点中,有一个点运动到终点时,所有运动即终止),设P、Q同时出发并运动了t秒.(1)当DQ=AP时,四边形APQD是平行四边形,求出此时t的值;
(2)当PQ将梯形ABCD分成一个平行四边形和一个等边三角形时,求t的值;
(3)试问是否存在这样的t,使四边形PBCQ的面积是梯形ABCD面积的一半?若存在,求出这样的t的值;若不存在,请说明理由.
分析:(1)由平行四边形对边相等的性质,求出t值;
(2)当PQ将梯形ABCD分成一个平行四边形和一个等边三角形时,即Q点运动到D点时,t值为3秒;
(3)先假设存在,求一下t的值,若符合题意则存在,不合题意则不存在.
(2)当PQ将梯形ABCD分成一个平行四边形和一个等边三角形时,即Q点运动到D点时,t值为3秒;
(3)先假设存在,求一下t的值,若符合题意则存在,不合题意则不存在.
解答:解:(1)∵四边形APQD是平行四边形,
∴DQ=AP,即3-t=2t,解得t=1(s),
(2)当PQ将梯形ABCD分成一个平行四边形和一个等边三角形时,Q点运动到D点,即
9-2t=3,解得t=3;
(3)假设存在这样的t值,使四边形PBCQ的面积是梯形ABCD面积的一半,即S梯形APQD=S梯形BPQC,
过点D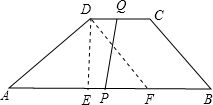 DE⊥AB,DF∥BC,
DE⊥AB,DF∥BC,
∴四边形BCDF是平行四边形,
∵AB=9cm,CD=3cm,AF=AB-BF=AB-CD=6cm,AD=BC=DF=6cm,
∴△ADF是等边三角形,
∴由勾股定理得DE=3
,
(3-t+2t)=
(t+9-2t),解得,t=3,
∴t=3时,四边形PBCQ的面积是梯形ABCD面积的一半.即(2)中的情况.
∴DQ=AP,即3-t=2t,解得t=1(s),
(2)当PQ将梯形ABCD分成一个平行四边形和一个等边三角形时,Q点运动到D点,即
9-2t=3,解得t=3;
(3)假设存在这样的t值,使四边形PBCQ的面积是梯形ABCD面积的一半,即S梯形APQD=S梯形BPQC,
过点D
 DE⊥AB,DF∥BC,
DE⊥AB,DF∥BC,∴四边形BCDF是平行四边形,
∵AB=9cm,CD=3cm,AF=AB-BF=AB-CD=6cm,AD=BC=DF=6cm,
∴△ADF是等边三角形,
∴由勾股定理得DE=3
| 3 |
3
| ||
| 2 |
3
| ||
| 2 |
∴t=3时,四边形PBCQ的面积是梯形ABCD面积的一半.即(2)中的情况.
点评:本题主要考查等腰梯形的性质的应用.还考查了动点问题,分类讨论的思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在,求出这样的t的值;若不存在,请说明理由.
在,求出这样的t的值;若不存在,请说明理由. 10、如图,在等腰梯形ABCD中,AD∥BC,AB=DC,E为AD的中点,求证:BE=CE.
10、如图,在等腰梯形ABCD中,AD∥BC,AB=DC,E为AD的中点,求证:BE=CE. 已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E、F分别在AB、DC上,且BE=3EA,CF=3FD.
已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E、F分别在AB、DC上,且BE=3EA,CF=3FD. (2012•广州)如图,在等腰梯形ABCD中,BC∥AD,AD=5,DC=4,DE∥AB交BC于点E,且EC=3,则梯形ABCD的周长是( )
(2012•广州)如图,在等腰梯形ABCD中,BC∥AD,AD=5,DC=4,DE∥AB交BC于点E,且EC=3,则梯形ABCD的周长是( )
