题目内容
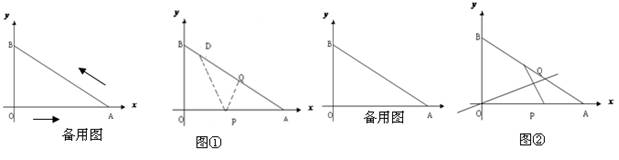
已知：如图，在等腰梯形ABCD中，AD∥BC，AB=DC，点E、F分别在AB、DC上，且BE=3EA，CF=3FD．求证：∠BEC=∠CFB．
分析：根据等腰梯形的性质得出∠ABC=∠DCB，根据已知求出BE=CF，根据SAS证出△EBC≌△FCB即可．
解答：证明：∵梯形ABCD中，AB=CD．
∴∠ABC=∠DCB．
∵BE=3EA，CF=3FD．
∴BE=
AB，CF=
CD．
∴BE=CF．
又∵BC=BC．
∴△EBC≌△FCB（SAS）．
∴∠BEC=∠CFB．
∴∠ABC=∠DCB．
∵BE=3EA，CF=3FD．
∴BE=
| 3 |
| 4 |
| 3 |
| 4 |
∴BE=CF．
又∵BC=BC．
∴△EBC≌△FCB（SAS）．
∴∠BEC=∠CFB．
点评：本题主要考查对等腰梯形的性质，全等三角形的性质和判定等知识点的理解和掌握，能求出△EBC≌△FCB是证此题的关键．
练习册系列答案
寒假学与练系列答案
相关题目
