题目内容
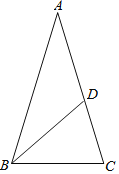
【题目】如图，已知△ABC，AB＝AC＝2，∠A＝36°，∠ABC的平分线BD交AC于点D，则cosA的值是_____．（结果保留根号）
【答案】
【解析】
通过证明△ABC∽△BDC，利用对应边成比例求出AD长，再作DE⊥AB于点E，利用三角函数求解即可.
解：∵△ABC，AB＝AC，∠A＝36°，
∴∠ABC＝∠ACB＝
＝72°．
∵BD是∠ABC的平分线，
∴∠ABD＝∠DBC＝
∠ABC＝36°．
∴∠A＝∠DBC＝36°，
又∵∠C＝∠C，
∴△ABC∽△BDC，
∴
＝
，
设AD＝x，则BD＝BC＝x．AB＝AC＝2，
则
＝
，
解得：x＝-1+
或x＝-1-（舍去）．
故x＝-1+．
如右图，过点D作DE⊥AB于点E，
∵AD＝BD，
∴E为AB中点，即AE＝AB＝1．
在Rt△AED中，cosA＝
＝
＝．
故答案是：．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
