题目内容
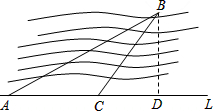如图：小军要测量河内小岛B到河岸L的距离，在A点测得∠BAD=30°，在C点测得∠BCD=60°，又测得AC=10米，则小岛B到河岸L的距离为（ ）A、5
| ||||
| B、5 | ||||
C、
| ||||
D、5+5
|
考点：解直角三角形的应用
专题：计算题
分析：根据三角形外角的性质和等角对等边易得AC=BC．那么利用60°的正弦函数可求得BD长，也就是小岛B到河岸L的距离．
解答：解：∵∠BAD=30°，∠BCD=60°，
∴∠ABC=30°，
∴BC=AC=10米，
∴BD=BC×sin60°=5
米．
故选：A．
∴∠ABC=30°，
∴BC=AC=10米，
∴BD=BC×sin60°=5
| 3 |
故选：A．
点评：考查了解直角三角形的应用，用到的知识点为：三角形的外角等于和它不相邻的两个内角的和；等角对等边；一个角的正弦值等于这个角所在的直角三角形中对边与斜边之比．
练习册系列答案
阅读快车系列答案
相关题目
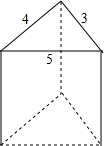如图是一个直三棱柱，则它的平面展开图中，错误的是（ ）A、 |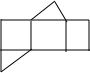
B、 |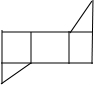
C、 |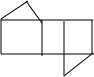
D、 |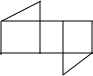
下列说法正确的是（ ）
| A、每个命题都有逆命题 |
| B、每个定理都有逆定理 |
| C、所有的命题都是定理 |
| D、假命题的逆命题是假命题 |
若a=-
，b=
，则a-b=（ ）
| 25 |
| 3 | -1 |
| A、4 | B、-4 | C、6 | D、-6 |
无论x取什么值，下列各式中总有意义的是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知圆⊙O1和⊙O2的半径的6cm和8cm，当O1O2=2cm时，⊙O1和⊙O2的位置关系为（ ）
| A、外切 | B、相交 | C、内切 | D、内含 |
两个有理数的和除以它们的积所得的商为零，则这两个数（ ）
| A、互为倒数 |
| B、互为相反数 |
| C、互为相反数且都不等于零 |
| D、互为倒数且都不等于零 |