题目内容

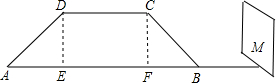如图是一座人行天桥，天桥的高12米，坡面的坡比为=1：1，为了方便行人推车过天桥，市政府决定降低坡度，使新的斜坡的坡角为30°，问离原坡底8米处的大型广告墙M要不要拆除？
分析：由原来的坡比求出CF的长度，然后根据新坡比求出FG，继而根据BG=FG-FB可得出BG的长度，与8米进行比较即可作出判断．
解答：解：∵坡面的坡比为1：1，

∴∠CBF=45°，
又∵CF=12米，则FB=12米，
由于新的斜坡的坡角为30°，如果坡底用字母G表示，
则CG=24米，FG=12
3
米，
故可得：BG=12
3
-12=8.784米＞8米，所以广告牌M要拆除．
点评：此题考查了解直角三角形的应用，理解坡比所表示的含义，求出线段BG的长度是解答本题的关键，难度一般，
练习册系列答案
相关题目
如图是一座人行天桥的引桥部分的示意图，上桥通道由两段互相平行并且与地面成37°精英家教网角的楼梯AD、BE和一段水平平台DE构成．已知天桥高度BC=4.8米，引桥水平跨度AC=8米．
（1）求水平平台DE的长度；
（2）若与地面垂直的平台立枉MN的高度为3米，求两段楼梯AD与BE的长度之比．
（参考数据：取sin37°=0.60，cos37°=0.80，tan37°=0.75．）
（2009•南安市质检）如图是一座人行天桥的示意图，天桥的高BC为10米，坡面AC的坡角为53°．
（1）求AB的长度．（精确到0.01米）
（2）为了方便行人推车过天桥，市政部门决定降低坡度，使新坡面DC的坡角为30°，且新的坡角外侧需留3米宽的人行道，问离原坡角12米的建筑物EF是否需要拆除？
（2012•江宁区二模）如图是一座人行天桥的示意图，天桥的高CB为10米，坡面CA的坡角为30°．为了方便行人推车过桥，市政部门决定降低坡度，使新坡面CD的坡角为18°，若新桥脚前需留4米的人行道，问离原坡脚15米的花坛是否需要拆除？请说明理由．
（参考数据：sinl8°≈0.3090，cosl8°≈0.9511，tanl8°≈0.3249，
2
≈1.414，
3
≈1.732）
（2012•潮阳区模拟）如图是一座人行天桥的引桥部分的示意图，上桥的通道由两段互相平行楼梯AD，BE和一段水平平台DE构成．已知∠A=37°，AD=5米，DE=1.6米，BE=3米，求天桥的高度BC和引桥的水平跨度AC的长（参考数据：取sin37°=0.60，cos37°=0.80，tan37°=0.75）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网