��Ŀ����
��֪���ھ���AOBC�У�OB=4��OA=3���ֱ���OB��OA����ֱ��Ϊx���y�ᣬ������ͼ��ʾ��ƽ��ֱ������ϵ��F�DZ�BC�ϵ�һ�����㣨����B��C�غϣ�����F��ķ���������y=| k | x |
��1����֤����AOE���BOF�������ȣ�
��2����S=S��OEF-S��ECF����kΪ��ֵʱ��S�����ֵ�����ֵΪ���٣�
��3����̽�����Ƿ���������ĵ�F��ʹ�ý���CEF��EF���ۺ�C��ǡ������OB�ϣ���
 ���ڣ������F�����ꣻ�������ڣ���˵�����ɣ�
���ڣ������F�����ꣻ�������ڣ���˵�����ɣ�
��������1���ֱ��õ�E��F�������ʾ����AOE���FOB����������бȽϣ�
��2��Ӧ�ֱ��þ������������ͼ�еĵ��ʾ���������ε������ʾ���������������ö��κ��������ֵ���ɣ�
��3����F�ĺ��������У����B�ĺ�������ͬ�������۵��Լ�������õ�F�������꣮
��2��Ӧ�ֱ��þ������������ͼ�еĵ��ʾ���������ε������ʾ���������������ö��κ��������ֵ���ɣ�
��3����F�ĺ��������У����B�ĺ�������ͬ�������۵��Լ�������õ�F�������꣮
���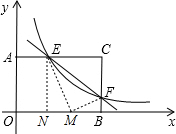 ��1��֤������E��x1��y1����F��x2��y2������AOE���FOB������ֱ�ΪS1��S2��
��1��֤������E��x1��y1����F��x2��y2������AOE���FOB������ֱ�ΪS1��S2��
�������y1=
��y2=
��
��S1=
x1y1=
k��S2=
x2y2=
k��
��S1=S2��
����AOE���FOB�������ȣ�
��2���⣺������֪E��F��������ֱ�ΪE��
��3����F��4��
����
��S��ECF=
EC•CF=
��4-
k����3-
k����
��S��EOF=S����AOBC-S��AOE-S��BOF-S��ECF
=12-
k-
k-S��ECF
=12-k-S��ECF
��S=S��OEF-S��ECF=12-k-2S��ECF=12-k-2��
��4-
k����3-
k����
��S=-
k2+k����S=-
��k-6��2+3��
��k=6ʱ��S�����ֵ��
S���ֵ=3��
��3���⣺����������ĵ�F������CEF��EF���ۺ�C��ǡ������OB���ϵ�M�㣬
����E��EN��OB������ΪN��
������ã�EN=AO=3��EM=EC=4-
k��MF=CF=3-
k��
�ߡ�EMN+��FMB=��FMB+��MFB=90�㣬
���EMN=��MFB��
�֡ߡ�ENM=��MBF=90�㣬
���EMN�ס�MFB��
��
=
��
��
=
=
��
��MB=
��
��MB2+BF2=MF2��
��(
)2+(
)2=(3-
k)2�����k=
��
��BF=
=
��
����ڷ��������ĵ�F����������Ϊ��4��
����
 ��1��֤������E��x1��y1����F��x2��y2������AOE���FOB������ֱ�ΪS1��S2��
��1��֤������E��x1��y1����F��x2��y2������AOE���FOB������ֱ�ΪS1��S2���������y1=
| k |
| x1 |
| k |
| x2 |
��S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��S1=S2��
����AOE���FOB�������ȣ�
��2���⣺������֪E��F��������ֱ�ΪE��
| k |
| 3 |
| k |
| 4 |
��S��ECF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
��S��EOF=S����AOBC-S��AOE-S��BOF-S��ECF
=12-
| 1 |
| 2 |
| 1 |
| 2 |
=12-k-S��ECF
��S=S��OEF-S��ECF=12-k-2S��ECF=12-k-2��
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
��S=-
| 1 |
| 12 |
| 1 |
| 12 |
��k=6ʱ��S�����ֵ��
S���ֵ=3��
��3���⣺����������ĵ�F������CEF��EF���ۺ�C��ǡ������OB���ϵ�M�㣬
����E��EN��OB������ΪN��
������ã�EN=AO=3��EM=EC=4-
| 1 |
| 3 |
| 1 |
| 4 |
�ߡ�EMN+��FMB=��FMB+��MFB=90�㣬
���EMN=��MFB��
�֡ߡ�ENM=��MBF=90�㣬
���EMN�ס�MFB��
��
| EN |
| MB |
| EM |
| MF |
��
| 3 |
| MB |
4-
| ||
3-
|
4(1-
| ||
3(1-
|
��MB=
| 9 |
| 4 |
��MB2+BF2=MF2��
��(
| 9 |
| 4 |
| k |
| 4 |
| 1 |
| 4 |
| 21 |
| 8 |
��BF=
| k |
| 4 |
| 21 |
| 32 |
����ڷ��������ĵ�F����������Ϊ��4��
| 21 |
| 32 |
�����������ۺ��ԱȽ�ǿ���ѷ�����������ͼ������ʣ�ͼ�ε�������㣬���κ�����ֵ�ļ�����ھ��εı����У��ۺ�������Щ֪ʶ������⣮��������ϵ��һ�������ε������ͨ������Ϊ���������ȥ����ֱ�������ε��������ʽ��

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
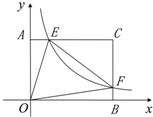 ��ֱ������ϵ������F�DZ�BC�ϵ�һ�����㣨����B��C�غϣ�����F��ķ���������y=
��ֱ������ϵ������F�DZ�BC�ϵ�һ�����㣨����B��C�غϣ�����F��ķ���������y=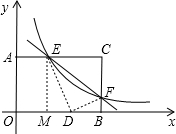 ��֪���ھ���AOBC�У�OB=4��OA=3���ֱ���OB��OA����ֱ��Ϊx���y�ᣬ������ͼ��ʾ��ƽ��ֱ������ϵ��F�DZ�BC�ϵ�һ�����㣨����B��C�غϣ�����F��ķ���������
��֪���ھ���AOBC�У�OB=4��OA=3���ֱ���OB��OA����ֱ��Ϊx���y�ᣬ������ͼ��ʾ��ƽ��ֱ������ϵ��F�DZ�BC�ϵ�һ�����㣨����B��C�غϣ�����F��ķ���������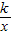 ��k��0����ͼ����߽��ڵ�E��
��k��0����ͼ����߽��ڵ�E��
 ��k��0����ͼ����AC�߽��ڵ�E.
��k��0����ͼ����AC�߽��ڵ�E.