题目内容
已知:在矩形AOBC中,OB=3,OA=2.分别以OB、OA所在直线为x轴和y轴,建立如图所示的平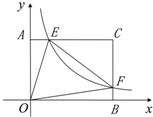 面直角坐标系.若点F是边BC上的一个动点(不与B、C重合),过F点的反比例函数y=
面直角坐标系.若点F是边BC上的一个动点(不与B、C重合),过F点的反比例函数y=| k | x |
(1)直接写出线段AE、BF的长(用含k的代数式表示);
(2)记△OEF的面积为S.
①求出S与k的函数关系式并写出自变量k的取值范围;
②以OF为直径作⊙N,若点E恰好在⊙N上,请求出此时△OEF的面积S.
分析:(1)从图象上可以得到E点的纵坐标为2,代入到反比例函数的解析式求得其横坐标即可,F点的横坐标为3,代入函数解析式求得其纵坐标即可;
(2)①用K表示出CE、CF,利用S是四边形和几个三角形的面积的差表示出S即可;
②证得△AOE∽△CEF后,得到比例式,进而得到有关K的一元二次方程求得K的值代入到①中求面积即可.
(2)①用K表示出CE、CF,利用S是四边形和几个三角形的面积的差表示出S即可;
②证得△AOE∽△CEF后,得到比例式,进而得到有关K的一元二次方程求得K的值代入到①中求面积即可.
解答:解:(1)AE=
,BF=
;
(2)①依题意得:CE=AC-AE=3-
,
CF=BC-BF=2-
,
∴S=S四边形OACB-S△CEF-S△OAE-S△OBF
=6-
(3-
)(2-
)-
k-
k
=-
k2+3.
其中0<k<6.
②∵OF为⊙N的直径,
∴∠FEO=90°.
∵∠OAE=90°,
∴∠AOE+∠AEO=∠CEF+∠AEO=90°.
∴∠AOE=∠CEF.
∵∠OAE=∠C=90°.
∴△AOE∽△CEF
∴
=
,
即
=
,
整理得:-3k2+26k=48,
解得:k1=
,k2=6(不合,舍去).
∴当k=
时,S=-
×(
)2+3=
| k |
| 2 |
| k |
| 3 |
(2)①依题意得:CE=AC-AE=3-
| k |
| 2 |
CF=BC-BF=2-
| k |
| 3 |
∴S=S四边形OACB-S△CEF-S△OAE-S△OBF
=6-
| 1 |
| 2 |
| k |
| 2 |
| k |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 12 |
其中0<k<6.
②∵OF为⊙N的直径,
∴∠FEO=90°.
∵∠OAE=90°,
∴∠AOE+∠AEO=∠CEF+∠AEO=90°.
∴∠AOE=∠CEF.
∵∠OAE=∠C=90°.
∴△AOE∽△CEF
∴
| AE |
| AO |
| CF |
| CE |
即
| k |
| 4 |
2-
| ||
3-
|
整理得:-3k2+26k=48,
解得:k1=
| 8 |
| 3 |
∴当k=
| 8 |
| 3 |
| 1 |
| 12 |
| 8 |
| 3 |
| 65 |
| 27 |
点评:本题是一道反比例函数的综合题,题目中还考查了比例式的证明及相似三角形的判定的知识,难度中等.

练习册系列答案
相关题目
 存在,求出点F的坐标;若不存在,请说明理由.
存在,求出点F的坐标;若不存在,请说明理由.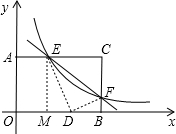 已知:在矩形AOBC中,OB=4,OA=3.分别以OB、OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数
已知:在矩形AOBC中,OB=4,OA=3.分别以OB、OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数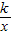 (k>0)的图象与边交于点E.
(k>0)的图象与边交于点E.
 (k>0)的图象与AC边交于点E.
(k>0)的图象与AC边交于点E.