��Ŀ����
��ͼ����B1��1��y1����B2��2��y2����B3��3��y3������Bn��n��yn����n��������������Ϊһ�κ���y=| 1 |
| 4 |
| 1 |
| 12 |
��1��д��B2��Bn��������ꣻ
��2����x2��x3���ú�a�Ĵ���ʽ��ʾ��������ͼ���и����������εױ߳���֮��Ĺ�ϵ��д������Ϊ�������������ۣ�
��3����a��0��a��1���仯ʱ�����������еĵ����������У��Ƿ����ֱ�������Σ������ڣ������Ӧ��a��ֵ���������ڣ���˵�����ɣ�
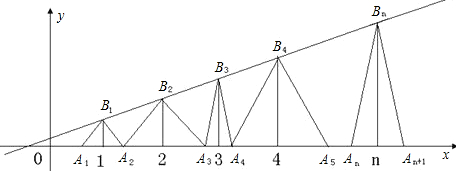
��������1����Ϊ��B1��1��y1����B2��2��y2����B3��3��y3������Bn��n��yn����n��������������Ϊһ�κ���y=
x+
��ͼ���ϵĵ㣬���Էֱ���x=2��x=n�������Ӧ��yֵ���ɣ�
��2����Ϊ��A1B1A2����A2B2A3����A3B3A4����AnBnAn+1�ֱ�����B1��B2��B3������BnΪ����ĵ��������Σ����õ��������εױ��ϵĸߴ�ֱƽ�ֵױߣ���֪x2-1=1-x1��x3-2=2-x2������x1=a������x2=2-a��x3=4-x2=2+a��
����ͼ���и����������εױ߳���֮��Ĺ�ϵʱ�������������������ΪB1��B3��B5��������λ���ϵĵ��������εױ߳�������2-2a������ΪB2��B4��B6����ż��λ���ϵĵ��������εױ߳�������2a��
��3�������n������������ǡ��Ϊֱ�������Σ���ô��������εĵױߵ��ڸ�yn��2�����ɵڣ�2��С��Ľ��ۿ�֪��
��nΪ����ʱ����2-2a=2��
+
)������õ���a��ʾn��ʽ�ӣ����a��ȡֵ��Χ�����n��ȡֵ��Χ������n�����������������n��ֵ����nΪż��ʱ����2a=2��
+
)��ͬ������õ���a��ʾn��ʽ�ӣ����a��ȡֵ��Χ�����n��ȡֵ��Χ������n�����������������n��ֵ��
| 1 |
| 4 |
| 1 |
| 12 |
��2����Ϊ��A1B1A2����A2B2A3����A3B3A4����AnBnAn+1�ֱ�����B1��B2��B3������BnΪ����ĵ��������Σ����õ��������εױ��ϵĸߴ�ֱƽ�ֵױߣ���֪x2-1=1-x1��x3-2=2-x2������x1=a������x2=2-a��x3=4-x2=2+a��
����ͼ���и����������εױ߳���֮��Ĺ�ϵʱ�������������������ΪB1��B3��B5��������λ���ϵĵ��������εױ߳�������2-2a������ΪB2��B4��B6����ż��λ���ϵĵ��������εױ߳�������2a��
��3�������n������������ǡ��Ϊֱ�������Σ���ô��������εĵױߵ��ڸ�yn��2�����ɵڣ�2��С��Ľ��ۿ�֪��
��nΪ����ʱ����2-2a=2��
| n |
| 4 |
| 1 |
| 12 |
| n |
| 4 |
| 1 |
| 12 |
����⣺��1��B2(2��
)��Bn(n��
+
)��
��2��x2=2-a��x3=2+a��
����1������ΪB1��B3��B5��������λ���ϵĵ��������εױ߳�������2-2a��
����2������ΪB2��B4��B6����ż��λ���ϵĵ��������εױ߳�������2a��
����3��ÿ���ڵ��������������εױ�֮�Ͷ����ڳ���2��
��3�����n������������ǡ��Ϊֱ�������Σ���ô��������εĵױߵ��ڸ�yn��2�����ɵڣ�2��С��Ľ��ۿ�֪��
��nΪ����ʱ����2-2a=2��
+
)������ã�n=-4a+
(0��a��1)��
��-
��n��
����n=1��3
��a=
��
��
��nΪż��ʱ����2a=2(
+
)���ã�n=4a-
(0��a��1)��
��-
��n��
����n=2
��a=
��
��������������ֱ�������Σ���a=
��
��
��
| 7 |
| 12 |
| n |
| 4 |
| 1 |
| 12 |
��2��x2=2-a��x3=2+a��
����1������ΪB1��B3��B5��������λ���ϵĵ��������εױ߳�������2-2a��
����2������ΪB2��B4��B6����ż��λ���ϵĵ��������εױ߳�������2a��
����3��ÿ���ڵ��������������εױ�֮�Ͷ����ڳ���2��
��3�����n������������ǡ��Ϊֱ�������Σ���ô��������εĵױߵ��ڸ�yn��2�����ɵڣ�2��С��Ľ��ۿ�֪��
��nΪ����ʱ����2-2a=2��
| n |
| 4 |
| 1 |
| 12 |
| 11 |
| 3 |
��-
| 1 |
| 3 |
| 11 |
| 3 |
��a=
| 2 |
| 3 |
| 1 |
| 6 |
��nΪż��ʱ����2a=2(
| n |
| 4 |
| 1 |
| 12 |
| 1 |
| 3 |
��-
| 1 |
| 3 |
| 11 |
| 3 |
��a=
| 7 |
| 12 |
��������������ֱ�������Σ���a=
| 2 |
| 3 |
| 1 |
| 6 |
| 7 |
| 12 |
�������������������ν�ϵ�˼�룬�������һ�κ���ͬ���������ε�������������⣮

��ϰ��ϵ�д�
�����Ŀ
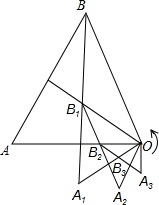 ��2013•��Ϫ����ͼ����B1�����Ϊ1�ĵȱߡ�OBA���������ߵĽ��㣬��OB1Ϊһ�ߣ�����ȱߡ�OB1A1����O��B1��A1����ʱ�뷽�����У�����Ϊ��һ�ι��죻��B2�ǡ�OB1A1���������ߵĽ��㣬����OB2Ϊһ�ߣ�����ȱߡ�OB2A2����O��B2��A2����ʱ�뷽�����У�����Ϊ�ڶ��ι��죻�Դ����ƣ�����n�ι�����ĵȱߡ�OBnAn�ı�OAn��ȱߡ�OBA�ı�OB��һ���غ�ʱ������ֹͣ������������һ�������ε������
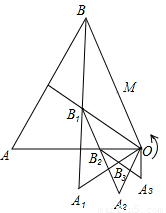
��2013•��Ϫ����ͼ����B1�����Ϊ1�ĵȱߡ�OBA���������ߵĽ��㣬��OB1Ϊһ�ߣ�����ȱߡ�OB1A1����O��B1��A1����ʱ�뷽�����У�����Ϊ��һ�ι��죻��B2�ǡ�OB1A1���������ߵĽ��㣬����OB2Ϊһ�ߣ�����ȱߡ�OB2A2����O��B2��A2����ʱ�뷽�����У�����Ϊ�ڶ��ι��죻�Դ����ƣ�����n�ι�����ĵȱߡ�OBnAn�ı�OAn��ȱߡ�OBA�ı�OB��һ���غ�ʱ������ֹͣ������������һ�������ε������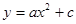 �Ķ��㣬��A1��A2���ڸ��������ϣ��ı���OA1B1C1��OA2B2C2��Ϊ�����Σ���B2��y���ϣ�ֱ��C2B2��������߽��ڵ�
�Ķ��㣬��A1��A2���ڸ��������ϣ��ı���OA1B1C1��OA2B2C2��Ϊ�����Σ���B2��y���ϣ�ֱ��C2B2��������߽��ڵ�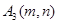 ����
����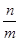 ��ֵ�� ��
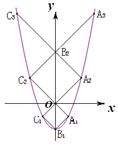
��ֵ�� �� 
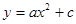 �Ķ��㣬��A1��A2���ڸ��������ϣ��ı���OA1B1C1��OA2B2C2��Ϊ�����Σ���B2��y���ϣ�ֱ��C2B2��������߽��ڵ�
�Ķ��㣬��A1��A2���ڸ��������ϣ��ı���OA1B1C1��OA2B2C2��Ϊ�����Σ���B2��y���ϣ�ֱ��C2B2��������߽��ڵ�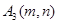 ����
����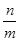 ��ֵ�� ��
��ֵ�� ��
