题目内容
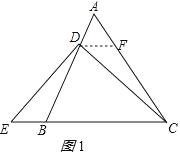
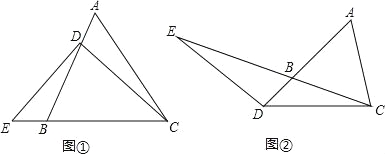
【题目】(2016山东省聊城市第29题)(1)、已知：△ABC是等腰三角形，其底边是BC，点D在线段AB上，E是直线BC上一点，且∠DEC=∠DCE，若∠A=60°（如图①）．求证：EB=AD；
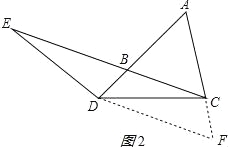
(2)、若将（1）中的“点D在线段AB上”改为“点D在线段AB的延长线上”，其它条件不变（如图②），（1）的结论是否成立，并说明理由；
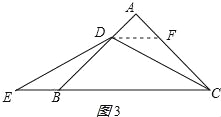
(3)、若将（1）中的“若∠A=60°”改为“若∠A=90°”，其它条件不变，则
的值是多少？（直接写出结论，不要求写解答过程）
【答案】(1)、证明过程见解析；(2)、成立；理由见解析；(3)、
【解析】
试题分析：(1)、作DF∥BC交AC于F，由平行线的性质得出∠ADF=∠ABC，∠AFD=∠ACB，∠FDC=∠DCE，证明△ABC是等边三角形，得出∠ABC=∠ACB=60°，证出△ADF是等边三角形，∠DFC=120°，得出AD=DF，由已知条件得出∠FDC=∠DEC，ED=CD，由AAS证明△DBE≌△CFD，得出EB=DF，即可得出结论；(2)、作DF∥BC交AC的延长线于F，同（1）证出△DBE≌△CFD，得出EB=DF，即可得出结论； (3)、作DF∥BC交AC于F，同（1）得：△DBE≌△CFD，得出EB=DF，证出△ADF是等腰直角三角形，得出DF=
AD，即可得出结果．
试题解析：(1)、作DF∥BC交AC于F，如图1所示：则∠ADF=∠ABC，∠AFD=∠ACB，∠FDC=∠DCE，
∵△ABC是等腰三角形，∠A=60°，∴△ABC是等边三角形，∴∠ABC=∠ACB=60°，
∴∠DBE=120°，∠ADF=∠AFD=60°=∠A，∴△ADF是等边三角形，∠DFC=120°， ∴AD=DF，
∵∠DEC=∠DCE， ∴∠FDC=∠DEC，ED=CD， ∴△DBE≌△CFD（AAS）， ∴EB=DF， ∴EB=AD；
(2)、EB=AD成立；理由如下：作DF∥BC交AC的延长线于F，如图2所示：
同（1）得：AD=DF，∠FDC=∠ECD，∠FDC=∠DEC，ED=CD，又∵∠DBE=∠DFC=60°，∴△DBE≌△CFD（AAS），∴EB=DF， ∴EB=AD；
(3)、
；理由如下：作DF∥BC交AC于F，如图3所示： 同（1）得：△DBE≌△CFD（AAS），
∴EB=DF，∵△ABC是等腰直角三角形，DF∥BC， ∴△ADF是等腰直角三角形， ∴DF=AD，
∴
， ∴．
