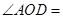题目内容
如图,AB是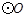 的直径,点C是半圆的中点,动点P在弦BC上,则
的直径,点C是半圆的中点,动点P在弦BC上,则 可能为( )
可能为( )
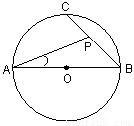
A.90° B.50° C.46° D.26°
【答案】
D
【解析】
试题分析:连接AC,根据圆周角定理可得∠ACB为直角,再由点C是半圆的中点可得△ABC为等腰直角三角形,根据等腰直角三角形的性质即可作出判断.
连接AC

则∠ACB=90°
∵点C是半圆的中点
∴AC=BC
∴∠CAB=∠CBA=45°
∴
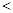 ∠CAB
∠CAB
∴ 可能为26°
可能为26°
故选D.
考点:圆周角定理,等腰直角三角形的判定和性质
点评:圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,均等于所对圆心角的一半.

练习册系列答案
相关题目
如图,AB是 的直径,点C是半圆的中点,动点P在弦BC上,则
的直径,点C是半圆的中点,动点P在弦BC上,则 可能为( )
可能为( )
| A.90° | B.50° | C.46° | D.26° |
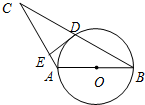 13、如图,AB是的⊙O直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,需添加的条件是
13、如图,AB是的⊙O直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,需添加的条件是
 的直径,点C、D在
的直径,点C、D在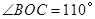 ,
,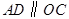 ,则
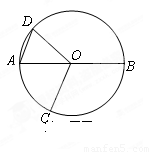
,则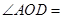 ( )
( )
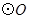 的直径,点C、D在
的直径,点C、D在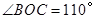 ,
,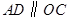 ,则
,则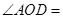
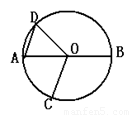
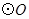 的直径,点C、D在
的直径,点C、D在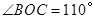 ,
,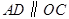 ,则
,则