题目内容
 如图,已知直线l1的解析式为y=3x+6,直线l1与x轴、y轴分别相交于A、B两点,直线l2经过B、C两点,点C的坐标为(8,0),点D是AC的中点,点Q从点C沿△BOC的三边按逆时针方向以每秒1个单位长度的速度运动一周,设移动时间为t秒
如图,已知直线l1的解析式为y=3x+6,直线l1与x轴、y轴分别相交于A、B两点,直线l2经过B、C两点,点C的坐标为(8,0),点D是AC的中点,点Q从点C沿△BOC的三边按逆时针方向以每秒1个单位长度的速度运动一周,设移动时间为t秒(1)求直线l2的解析式;
(2)设△DCQ的面积为S,请求出S关于t的函数关系式,并写出t的取值范围;
(3)试探究:点P在x轴上以每秒1个单位长度的速度从点A向点C运动,若点P与点Q同时出发,当其中一个点到达终点时,另一点也随之停止运动,t为何值时,以点P、Q、C为顶点的三角形与△BOC相似.
分析:(1)利用已知得出B,C点的坐标,再利用待定系数法求一次函数解析式即可;
(2)根据当0<t≤10时以及当10<t<16时,分别求出QE的长即可得出答案;
(3)根据当过点P作PQ⊥BC于点Q时,当QP⊥OC于点C时,分别利用相似三角形的判定与性质得出t的值即可.
(2)根据当0<t≤10时以及当10<t<16时,分别求出QE的长即可得出答案;
(3)根据当过点P作PQ⊥BC于点Q时,当QP⊥OC于点C时,分别利用相似三角形的判定与性质得出t的值即可.
解答: 解:(1)由题意,知B(0,6),C(8,0),
解:(1)由题意,知B(0,6),C(8,0),
设直线l2的解析式为y=kx+b,则
,
解得:
,
故l2的解析式为:y=-
x+6;
(2)如图1,过点Q作QE⊥OC于点E,
当0<t≤10时,
∵QE⊥CO,
∴∠QEC=90°,
∴BO∥QE,
∴△CBO∽△CQE,
∴
=
,
∵BO=6,CO=8,
∴BC=
=10,
QC=t,
∴
=
,
解得:QE=
t,
∵直线l1的解析式为y=3x+6,直线l1与x轴相交于A点,
∴x=-2,
∴AO=2,则AC=2+8=10,即DC=5,
∴△DCQ的面积为:S=
×5×
t=
t,
如图2,当10<t<16时,
∵QO=16-t,DC=5,
∴△DCQ的面积为:S=
×5×(16-t)=-
t+40;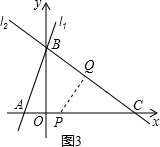
(3)如图3,当过点P作PQ⊥BC于点Q时,
∵∠PQC=90°,∠BOC=90°,∠QCP=OCB,
∴△BOC∽△PQC,
∴
=
,
∴
=
,
解得:t=
,
如图4,当QP⊥OC于点C时,
∵QP⊥CO,BO⊥CO,
∴QP∥BO,
∴△QPC∽△BOC,
∴
=
,
∴
=
,
解得:t=
,
综上所述:当t=
,
时,以点P、Q、C为顶点的三角形与△BOC相似.
 解:(1)由题意,知B(0,6),C(8,0),
解:(1)由题意,知B(0,6),C(8,0),设直线l2的解析式为y=kx+b,则
|
解得:
|
故l2的解析式为:y=-
| 3 |
| 4 |
(2)如图1,过点Q作QE⊥OC于点E,
当0<t≤10时,
∵QE⊥CO,
∴∠QEC=90°,
∴BO∥QE,
∴△CBO∽△CQE,
∴
| OB |
| QE |
| BC |
| QC |
∵BO=6,CO=8,
∴BC=
| 62+82 |
QC=t,

∴
| 6 |
| QE |
| 10 |
| t |
解得:QE=
| 3 |
| 5 |
∵直线l1的解析式为y=3x+6,直线l1与x轴相交于A点,
∴x=-2,
∴AO=2,则AC=2+8=10,即DC=5,
∴△DCQ的面积为:S=
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 2 |
如图2,当10<t<16时,
∵QO=16-t,DC=5,
∴△DCQ的面积为:S=
| 1 |
| 2 |
| 5 |
| 2 |

(3)如图3,当过点P作PQ⊥BC于点Q时,
∵∠PQC=90°,∠BOC=90°,∠QCP=OCB,
∴△BOC∽△PQC,
∴
| QC |
| CO |
| PC |
| BC |
∴
| t |
| 8 |
| 10-t |
| 10 |
解得:t=
| 40 |
| 9 |
如图4,当QP⊥OC于点C时,

∵QP⊥CO,BO⊥CO,
∴QP∥BO,
∴△QPC∽△BOC,
∴
| QC |
| BC |
| PC |
| CO |
∴
| t |
| 10 |
| 10-t |
| 8 |
解得:t=
| 50 |
| 9 |
综上所述:当t=
| 40 |
| 9 |
| 50 |
| 9 |
点评:此题主要考查了一次函数的综合应用以及相似三角形的判定与性质和待定系数法求一次函数解析式等知识,利用数形结合以及分类讨论得出是解题关键.

练习册系列答案
相关题目
 向点B移动.点P,Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t秒(1<t<10).
向点B移动.点P,Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t秒(1<t<10).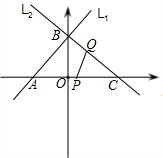 直线L2从点C向点B移动(一点到达终点,另一点即停止运动).点P、Q同时出发,移动的速度都为每秒1个单位长度,设移动时间为t秒.
直线L2从点C向点B移动(一点到达终点,另一点即停止运动).点P、Q同时出发,移动的速度都为每秒1个单位长度,设移动时间为t秒. 如图,已知直线l1的解析式为y=3x+6,直线l1,与x轴、y轴分别相交于A,B两点,直线l2经过B,C两点,点C的坐标为(8,0).又已知点P在x轴上从点A向点C移动,点Q在直线l2上从点C向点B移动,点P,Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t s(1<t<10).
如图,已知直线l1的解析式为y=3x+6,直线l1,与x轴、y轴分别相交于A,B两点,直线l2经过B,C两点,点C的坐标为(8,0).又已知点P在x轴上从点A向点C移动,点Q在直线l2上从点C向点B移动,点P,Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t s(1<t<10).