题目内容
已知两直线L1：y=k1x+b1，L2：y=k2x+b2，若L1⊥L2，则有k1•k2=﹣1．
（1）应用：已知y=2x+1与y=kx﹣1垂直，求k；
（2）直线经过A（2，3），且与y=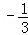
x+3垂直，求解析式．
（1）应用：已知y=2x+1与y=kx﹣1垂直，求k；
（2）直线经过A（2，3），且与y=
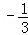x+3垂直，求解析式．(1)k=﹣
；
(2)解析式为y=3x﹣3．
；(2)解析式为y=3x﹣3．
试题分析：（1）根据L1⊥L2，则k1•k2=﹣1，即可得出k的值；
（2）根据直线互相垂直，则k1•k2=﹣1，可得出过点A的直线的k值等于3，由待定系数法即可得出所求的解析式
试题解析：（1）∵L1⊥L2，则k1•k2=﹣1，
∴2k=﹣1，
∴k=﹣
；（2）∵过点A直线与y=
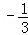x+3垂直，∴设过点A直线的直线解析式为y=3x+b，
把A（2，3）代入得，b=﹣3，
∴解析式为y=3x﹣3．
练习册系列答案
阅读快车系列答案
相关题目
在第一象限内的图象交于点B（m，n），连结OB．若S△AOB=6，S△BOC=2．
，0），且与反比例函数y=
（m≠0）的图象相交于点A（﹣2，1）和点B．
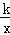的图象交于点A（1，m）和点B．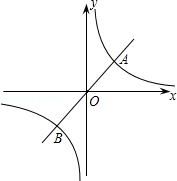
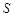（单位：平方米）与工作时间
（单位：小时）的函数关系的图象如图所示，则休息后园林队每小时绿化面积为