题目内容
一个多边形的内角和是它外角和的4倍,求这个多边形的边数及该多边形对角线的总条数.
解:设这个正多边形的边数是n,则
(n-2)•180°=1440°,
解得:n=10.
则从这个多边形一个顶点可以引7条对角线,
故这个多边形的总条数为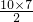 =35条.
=35条.
分析:一个多边形的内角和等于外角和的4倍而任何多边形的外角和是360°,因而多边形的内角和等于1440°.n边形的内角和可以表示成(n-2)•180°,设这个正多边形的边数是n,就得到方程,从而求出边数,即可求出答案.
点评:本题主要考查多边形内角与外角的知识点,此题比较简单,只要结合多边形的内角和公式寻求等量关系,构建方程求解即可.
从n边形一个顶点可以引n-3条对角线.
(n-2)•180°=1440°,
解得:n=10.
则从这个多边形一个顶点可以引7条对角线,
故这个多边形的总条数为
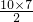 =35条.
=35条.分析:一个多边形的内角和等于外角和的4倍而任何多边形的外角和是360°,因而多边形的内角和等于1440°.n边形的内角和可以表示成(n-2)•180°,设这个正多边形的边数是n,就得到方程,从而求出边数,即可求出答案.
点评:本题主要考查多边形内角与外角的知识点,此题比较简单,只要结合多边形的内角和公式寻求等量关系,构建方程求解即可.
从n边形一个顶点可以引n-3条对角线.

练习册系列答案
相关题目