题目内容
 说理填空:如图直线a、b被直线c、d所截,且a∥b,∠1=70°,∠5=50°,这时∠2,∠3,∠4各是多少度?为什么?
说理填空:如图直线a、b被直线c、d所截,且a∥b,∠1=70°,∠5=50°,这时∠2,∠3,∠4各是多少度?为什么?
解:因为a∥b(已知),
所以∠1=∠2(________),
因为∠1=70°(已知),
所以∠2=70°.
因为a∥b(________),
所以∠3+________=180°(________ ),
因为∠5=50°(已知)
所以∠3=________(________ )
所以∠3=∠4=180°-50°=130°.
两直线平行内错角相等 已知 ∠5 两直线平行同旁内角互补 130° 等式的性质
分析:由a与b平行,利用两直线平行内错角相等得到一对角相等,进而由∠1的度数确定出∠2等式,再由a与b平行,利用两直线平行同旁内角互补,得到一对角互补,由∠5的度数求出∠3的度数,再由两直线平行同位角相等,可得出∠4的度数.
解答:因为a∥b(已知),
所以∠1=∠2(两直线平行内错角相等),
因为∠1=70°(已知),
所以∠2=70°.
因为a∥b(已知),
所以∠3+∠5=180°(两直线平行同旁内角互补),
因为∠5=50°(已知)
所以∠3=130°(等式的性质),
所以∠3=∠4=180°-50°=130°.
点评:此题考查了平行线的判定与性质,属于推理型填空题,熟练掌握平行线的判定与性质是解本题的关键.
分析:由a与b平行,利用两直线平行内错角相等得到一对角相等,进而由∠1的度数确定出∠2等式,再由a与b平行,利用两直线平行同旁内角互补,得到一对角互补,由∠5的度数求出∠3的度数,再由两直线平行同位角相等,可得出∠4的度数.
解答:因为a∥b(已知),
所以∠1=∠2(两直线平行内错角相等),
因为∠1=70°(已知),
所以∠2=70°.
因为a∥b(已知),
所以∠3+∠5=180°(两直线平行同旁内角互补),
因为∠5=50°(已知)
所以∠3=130°(等式的性质),
所以∠3=∠4=180°-50°=130°.
点评:此题考查了平行线的判定与性质,属于推理型填空题,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 33、看图填空,并在括号内注明说理依据.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?
33、看图填空,并在括号内注明说理依据.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗? 说理填空:如图直线a、b被直线c、d所截,且a∥b,∠1=70°,∠5=50°,这时∠2,∠3,∠4各是多少度?为什么?
说理填空:如图直线a、b被直线c、d所截,且a∥b,∠1=70°,∠5=50°,这时∠2,∠3,∠4各是多少度?为什么?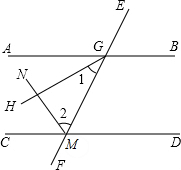 说理填空:如图,已知AB∥CD,GH平分∠AGM,MN平分∠CMG,请说明GH⊥MN的理由.
说理填空:如图,已知AB∥CD,GH平分∠AGM,MN平分∠CMG,请说明GH⊥MN的理由. 说理填空:如图,点E是DC的中点,EC=EB,∠CDA=120°,DF∥BE,且DF平分∠CDA,若△BCE的周长为18cm,求DC的长.
说理填空:如图,点E是DC的中点,EC=EB,∠CDA=120°,DF∥BE,且DF平分∠CDA,若△BCE的周长为18cm,求DC的长.