题目内容
【题目】在△ABC中,AB=10,AC=2 ![]() ,BC边上的高AD=6,则另一边BC等于( )
,BC边上的高AD=6,则另一边BC等于( )
A.10
B.8
C.6或10
D.8或10
【答案】C
【解析】解:根据题意画出图形,如图所示, 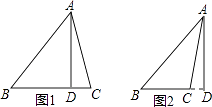
如图1所示,AB=10,AC=2 ![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD= ![]() =8,CD=
=8,CD= ![]() =2,
=2,
此时BC=BD+CD=8+2=10;
如图2所示,AB=10,AC=2 ![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD= ![]() =8,CD=
=8,CD= ![]() =2,此时BC=BD﹣CD=8﹣2=6,
=2,此时BC=BD﹣CD=8﹣2=6,
则BC的长为6或10.
故选C.
分两种情况考虑,如图所示,分别在直角三角形ABD与直角三角形ACD中,利用勾股定理求出BD与CD的长,即可求出BC的长.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目