题目内容
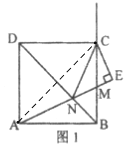
【题目】已知:正方形ABCD的边长为2,点M在射线BC上,且∠BAM=θ,射线AM交BD于点N,作CE⊥AM于点E.

(1)如图1,当点M在边BC上时,则θ的取值范围是(点M与端点B不重合) ;∠NCE与∠BAM的数量关系是 ;
(2)若点M在BC的延长线时;
①依题意,补全图2;
②(1)中的∠NCE与∠BAM的数量关系是否发生变化?若变化,写出数量关系,并说明理由.
【答案】(1)![]() ;
;![]() (或
(或![]() )(2)①图见解析;②变化:
)(2)①图见解析;②变化:![]() (或
(或![]() )
)
【解析】
(1)连接AC,根据∠BAC=45°解答即可求出![]() 的取值范围;通过证明△BAN≌△BCN可证明∠BAM=∠BCN,根据∠BAM+∠AMB=90°,∠ECM+∠CME=90°,∠AMB=∠CME可知∠BAM=∠ECM,即可证明
的取值范围;通过证明△BAN≌△BCN可证明∠BAM=∠BCN,根据∠BAM+∠AMB=90°,∠ECM+∠CME=90°,∠AMB=∠CME可知∠BAM=∠ECM,即可证明![]() ;(2)①根据题意画出图形即可;②连接AC,根据正方形的性质可证明AN=CN,即可证明∠NAC=∠NCA,根据外角性质及直角三角形两锐角互余即可求出∠NCE=180°-2∠BAN.
;(2)①根据题意画出图形即可;②连接AC,根据正方形的性质可证明AN=CN,即可证明∠NAC=∠NCA,根据外角性质及直角三角形两锐角互余即可求出∠NCE=180°-2∠BAN.
(1)连接AC,则∠BAC=45°,
∵M在BC上,不与B重合,
∴![]() ≤45°.
≤45°.
∵AB=BC,∠ABN=∠CBN=45°,BN=BN,
∴△BAN≌△BCN,
∴∠BAM=∠BCN,
∵∠BAM+∠AMB=90°,∠ECM+∠CME=90°,∠AMB=∠CME
∴∠BAM=∠ECM,
∴∠NCE=∠BCN+∠ECM=2∠BAM
故答案为:![]() ≤45°;
≤45°;![]() (或
(或![]() ).
).
(2)①补全图如下:

②有变化;∠NCE=180°-2∠BAN.理由如下:
如图:连接AC,
∵AC、BD是正方形ABCD的对角线,
∴NA=NC,
∴∠NAC=∠NCA,
∴∠ENC=2∠NAC,
∵∠NAC=∠BAN-45°,∠ENC=90°-∠NCE,
∴90°-∠NCE=2(∠BAN-45°)
∴∠NCE=180°-2∠BAN.(或![]() )
)