题目内容
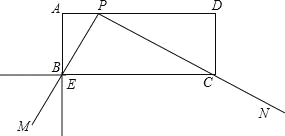
【题目】如图,在矩形ABCD中,AB=3,AD=10,将∠MPN的顶点P在矩形ABCD的边AD上滑动,在滑动过程中,始终保持∠MPN=90°,射线PN经过点C,射线PM交直线AB于点E,交直线BC于点F.
(1)求证:△AEP∽△DPC;
(2)在点P的运动过程中,点E与点B能重合吗?如果能重合,求DP的长;
(3)是否存在这样的点P使△DPC的面积等于△AEP面积的4倍?若存在,求出AP的长;若不存在,请证明理由.

【答案】(1)证明详见解析;(2)点E与点B能重合,B,E重合时DP的长为1或9;(3) 存在满足条件的点P,AP=1.5.
【解析】
试题分析:(1)根据矩形的性质,推出∠D=∠A=90°,再由直角三角形的性质,得出∠PCD+∠DPC=90°,又因∠CPE=90°,推出∠EPA+∠DPC=90°,∠PCD=∠EPA,从而证明△CDP∽△PAE;
(2)利用当B,E重合时,利用已知得出△ABP∽DPC,进而求出DP的长即可;
(3)假设存在满足条件的点P,设DP=x,则AP=10﹣x,由△CDP∽△PAE知,求出DP即可.
试题解析:(1)∵四边形ABCD是矩形,
∴∠D=∠A=90°,CD=AB=6,
∴∠PCD+∠DPC=90°,
又∵∠CPE=90°,
∴∠EPA+∠DPC=90°,
∴∠PCD=∠EPA,
∴△AEP∽△DPC;
(2)假设在点P的运动过程中,点E能与点B重合,
当B,E重合时,
∵∠BPC=90°,
∴∠APB+∠DPC=90°,
∵∠DPC+∠DCP=90°,
∴∠DCP=∠APB,
∵∠A=∠D,
∴△ABP∽DPC,
∴![]() ,
,
即![]() ,
,
解得:DP=1或9,
∴B,E重合时DP的长为1或9;
(3)存在满足条件的点P,
∵△CDP∽△PAE,
根据使△DPC的面积等于△AEP面积的4倍,得到两三角形的相似比为2,
∴![]() =2,
=2,
即![]() =2,
=2,
解得AP=1.5.

【题目】下表是某校九年级(1)班20名学生某次数学测验的成绩统计表:
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 1 | 5 | x | y | 2 |
(1)若这20名学生成绩的平均分数为82分,求x和y的值;
(2)在(1)的条件下,设这20名学生本次测验成绩的众数为a,中位数为b,求a,b的值.
【题目】某服装点用6000购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价﹣进价),这两种服装的进价,标价如表所示.
类型 | A型 | B型 |
进价(元/件) | 60 | 100 |
标价(元/件) | 100 | 160 |
(1)求这两种服装各购进的件数;
(2)如果A种服装按标价的8折出售,B种服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?