Question

【题目】我们知道：有两条边相等的三角形叫做等腰三角形．类似地，我们定义：至少有一组对边相等的四边形叫做等对边四边形．

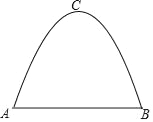
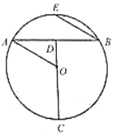
（1）如图，在中，点，分别在，上，设，相交于点，若，．请你写出图中一个与相等的角，并猜想图中哪个四边形是等对边四边形？

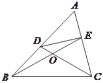
（2）在中，如果是不等于的锐角，点，分别在，上，且．探究：满足上述条件的图形中是否存在等对边四边形，并证明你的结论．

Answer 1

【答案】（1）与∠A相等的角是∠BOD、∠COE，四边形DBCE是等对边四边形；（2）存在等对边四边形DBCE，证明见解析；

【解析】

（1）根据三角形外角的性质可得∠BOD＝60°，根据对顶角的性质可得∠COE＝60°；作CG⊥BE于G点，作BF⊥C，D交CD延长线于F点通过证明△BCF≌△CBG，可得BF＝CG，,再证明△BDF≌△CEG，即可证明四边形DBCE是等对边四边形；

（2）作CG⊥BE于G点，作BF⊥CD交CD延长线于F点．易证△BCF≌△CBG，进而证明△BDF≌△CEG，所以BD＝CE，所以四边形DBCE是等对边四边形．

（1）∵∠A=60°，

∴∠OBC=∠OCB=30°

∴∠BOD＝∠COE=∠OBC＋∠OCB＝30°＋30°＝60°，

∴与∠A相等的角是∠BOD、∠COE，

四边形DBCE是等对边四边形，证明如下：

如图，作CG⊥BE于G点，作BF⊥CD交CD延长线于F点．

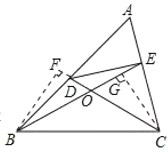
∴∠BFC=∠CGB=∠CGE=90°

∵∠DCB＝∠EBC＝∠A，BC=BC，

∴△BCF≌△CBG，

∴BF＝CG，

∵∠BDF＝∠ABE＋∠DOB，∠BEC＝∠ABE＋∠A，∠A=∠BOD

∴∠BDF＝∠BEC，

又∵∠BFD=∠CGE=90°，BF＝CG，

∴△BDF≌△CEG，

∴BD＝CE，

∴四边形DBCE是等对边四边形．

（2）存在等对边四边形DBCE，理由如下：

如图，作CG⊥BE于G点，作BF⊥CD交CD延长线于F点．

∴∠BFC=∠CGB=∠CGE=90°

∵∠DCB＝∠EBC＝∠A，BC=BC，

∴△BCF≌△CBG，

∴BF＝CG，

∵

∴∠BOD =∠OBC＋∠OCB＝ ，

∴∠A=∠BOD，

∵∠BDF＝∠ABE＋∠DOB，∠BEC＝∠ABE＋∠A，

∴∠BDF＝∠BEC，

又∵∠BDF=∠CGE=90°，BF＝CG，

∴△BDF≌△CEG，

∴BD＝CE，

∴四边形DBCE是等对边四边形．