题目内容
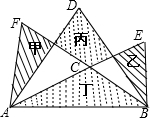 如图,以△ABC的每一条边为边作三个正三角形△ABD、△BCE和△ACF.已知这三个正三角形构成的图形中,甲、乙阴影部分的面积和等于丙、丁阴影部分的面积和,则∠FCE=
如图,以△ABC的每一条边为边作三个正三角形△ABD、△BCE和△ACF.已知这三个正三角形构成的图形中,甲、乙阴影部分的面积和等于丙、丁阴影部分的面积和,则∠FCE=
- A.130°
- B.140°
- C.150°
- D.160°
C
分析:先根据甲、乙阴影部分的面积和等于丙、丁阴影部分的面积和,可得出S△ACF+S△BCE=S△ABD,由勾股定理的逆定理可得出∠ACB=90°,进而可得出答案.
解答:由题意,得S△ACF+S△BCE=S△ABD,即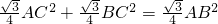 .
.
从而 AC2+BC2=AB2.
所以∠ACB=90°,∠FCE=360°-(90°+60°+60°)=150°.
故选C.
点评:本题考查的是勾股定理的逆定理、三角形的面积及等边三角形的性质,解答此题时要注意把三角形面积之间的关系转化为三边之间的关系,再由直角三角形及等边三角形的性质即可得出结论.
分析:先根据甲、乙阴影部分的面积和等于丙、丁阴影部分的面积和,可得出S△ACF+S△BCE=S△ABD,由勾股定理的逆定理可得出∠ACB=90°,进而可得出答案.
解答:由题意,得S△ACF+S△BCE=S△ABD,即
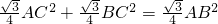 .
.从而 AC2+BC2=AB2.
所以∠ACB=90°,∠FCE=360°-(90°+60°+60°)=150°.
故选C.
点评:本题考查的是勾股定理的逆定理、三角形的面积及等边三角形的性质,解答此题时要注意把三角形面积之间的关系转化为三边之间的关系,再由直角三角形及等边三角形的性质即可得出结论.

练习册系列答案
相关题目
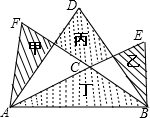 如图,以△ABC的每一条边为边作三个正三角形△ABD、△BCE和△ACF.已知这三个正三角形构成的图形中,甲、乙阴影部分的面积和等于丙、丁阴影部分的面积和,则∠FCE=( )
如图,以△ABC的每一条边为边作三个正三角形△ABD、△BCE和△ACF.已知这三个正三角形构成的图形中,甲、乙阴影部分的面积和等于丙、丁阴影部分的面积和,则∠FCE=( )| A、130° | B、140° | C、150° | D、160° |
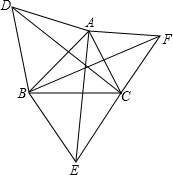
 14、已知:如图分别以△ABC的每一条边,在三角形外作等边三角形,△ABD、△BCE、△ACF,则CD=AE=BF.(
14、已知:如图分别以△ABC的每一条边,在三角形外作等边三角形,△ABD、△BCE、△ACF,则CD=AE=BF.(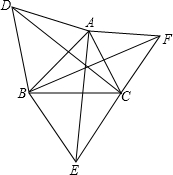 已知:如图分别以△ABC的每一条边,在三角形外作等边三角形,△ABD、△BCE、△ACF,则CD=AE=BF.
已知:如图分别以△ABC的每一条边,在三角形外作等边三角形,△ABD、△BCE、△ACF,则CD=AE=BF.