题目内容
（2013•扬州）矩形的两邻边长的差为2，对角线长为4，则矩形的面积为
6
6
．分析：设矩形一条边长为x，则另一条边长为x-2，然后根据勾股定理列出方程式求出x的值，继而可求出矩形的面积．
解答：解：设矩形一条边长为x，则另一条边长为x-2，
由勾股定理得，x2+（x-2）2=42，
整理得，x2-2x-6=0，
解得：x=1+
或x=1-
（不合题意，舍去），
另一边为：
-1，
则矩形的面积为：（1+
）（
-1）=6．
故答案为：6．
由勾股定理得，x2+（x-2）2=42，
整理得，x2-2x-6=0，
解得：x=1+
| 7 |
| 7 |
另一边为：
| 7 |
则矩形的面积为：（1+
| 7 |
| 7 |
故答案为：6．
点评：本题考查了勾股定理及矩形的性质，难度适中，解答本题的关键是根据勾股定理列出等式求处矩形的边长，要求同学们掌握矩形面积的求法．
练习册系列答案
相关题目
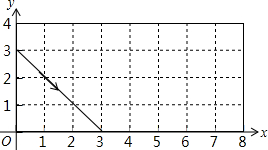（2013•德州）如图，动点P从（0，3）出发，沿所示方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，当点P第2013次碰到矩形的边时，点P的坐标为（ ）