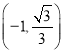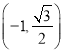题目内容
【题目】如图,一次函数 ![]() 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线 ![]() 过A、B两点.
过A、B两点.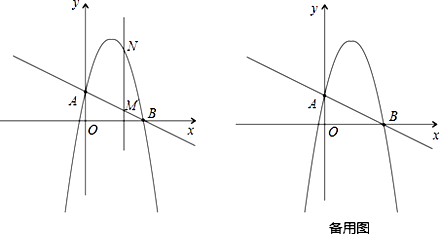
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N.求当t 取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
【答案】
(1)解:∵ ![]() 分别交y轴、x轴于A.、B两点,
分别交y轴、x轴于A.、B两点,
∴A、B点的坐标为:A(0,2),B(4,0),
将x=0,y=2代入y=x+bx+c得c=2,
将x=4,y=0,c=2代入y=x+bx+c得0=16+4b+2,解得b= ![]() ,
,
∴抛物线解析式为: ![]()
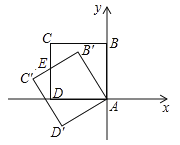
(2)解:如图1,
由题意可知,直线MN即是直线 ![]() ,
,
∵点M在直线 ![]() 上,点N在抛物线
上,点N在抛物线 ![]() 上,
上,
∴点M、N的坐标分别为 ![]() 、
、 ![]() ,
,
∵在第一象限中,点N在点M的上方,
∴MN= ![]() ,
,
∴当 ![]() 时,MN最长=4;
时,MN最长=4;
(3)解:由(2)可知,A(0,2),M(2,1),N(2,5).
以A. M、N、D为顶点作平行四边形,D点的可能位置有三种情形,如图2所示: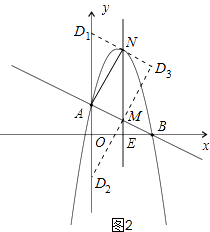
(i)当D在y轴上时,设D的坐标为(0,a)
由AD=MN,得|a2|=4,解得a1=6,a2=2,
从而D1为(0,6)或D2(0,2),
(ii)当D不在y轴上时,由图可知D3为D1N与D2M的交点,
由D1、D2、M、N的坐标可求得直线D1N的解析式为:y= ![]() x+6,直线D2M的解析式为:y=
x+6,直线D2M的解析式为:y= ![]() x2,
x2,
由 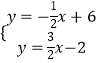 解得
解得 ![]() ,
,
∴D3的坐标为:(4,4),
综上所述,所求的D点坐标为(0,6),(0,2)或(4,4)
【解析】(1)先求出直线y=-![]() x+2与x轴、y轴的交点B、A的坐标,再将点A、B的坐标分别代入二次函数解析式,建立方程求出b、c的值,就可得出二次函数解析式。
x+2与x轴、y轴的交点B、A的坐标,再将点A、B的坐标分别代入二次函数解析式,建立方程求出b、c的值,就可得出二次函数解析式。
(2)根据直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N,可知点M、N的横坐标都为t,根据两函数解析式可得出两点的纵坐标,再根据MN=点N的纵坐标-点M的纵坐标,列出MN关于t的函数解析式,求出顶点坐标,即可得到MN有最大值时t的值即MN的长。
(3)抓住已知条件在(2)的情况下MN=4,要以A、M、N、D为顶点作平行四边形,根据点D的位置情况分两种:当(i)当D在y轴上时,设D的坐标为(0,a),根据MN=4即|a2|=4,求出a的值,得到点D的坐标由两个;(ii)当D不在y轴上时,即是以MN为平行四边形的对角线时,可知D3为D1N与D2M的交点,再求出直线D1N的解析式和直线D2M的解析式,然后将两一次函数解析式联立方程组求解即可得出点D的坐标。