题目内容
如图,平行四边ABCD中,O为AB上的一点,连接OD.OC,以O为圆心,OB为半径画圆,分别交OD,OC于点P.Q.若OB=4,OD=6,∠ADO=∠A, =2π,判断直线DC与⊙O的位置关系,并说明理由.
=2π,判断直线DC与⊙O的位置关系,并说明理由.

【答案】
直线DC与⊙O相离.理由见解析.
【解析】
试题分析:作OE⊥CD于点E,首先利用弧长公式求得圆心角∠COD的度数,得到△COD是直角三角形,根据三角形的面积公式即可求得OE的长,然后与半径的长度比较大小即可.
试题解析:如图, 在⊙O中,半径OB=4,
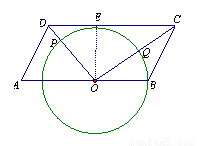
设∠POQ为n°,则有  .
.
∴n=90°.
∴∠POQ=90°.
∵∠ADO=∠A,
∴AO=DO=6.
∴AB=10.
∵四边形ABCD是平行四边形,
∴DC=AB=10.
∴ CO=8.?
过点O作OE⊥CD于点E,
则OD×OC=OE×CD.
∴OE=4.8.
∵4.8>4,
∴直线DC与⊙O相离.
考点:直线与圆的位置关系.

练习册系列答案
相关题目
 7、如图,要使平行四边行ABCD成为矩形,需添加的条件是( )
7、如图,要使平行四边行ABCD成为矩形,需添加的条件是( )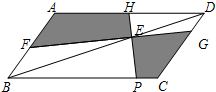 (2013•南京二模)如图,在?ABCD中,E是对角线BD上一点,过E点的线段FG、HP分别交平行四边形四边于F、G、H、P.若要使得图中两个阴影部分面积的大小关系是唯一确定的,则需要添加的条件是( )
(2013•南京二模)如图,在?ABCD中,E是对角线BD上一点,过E点的线段FG、HP分别交平行四边形四边于F、G、H、P.若要使得图中两个阴影部分面积的大小关系是唯一确定的,则需要添加的条件是( )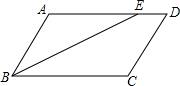 如图,平行四边ABCD中,BE平分∠ABC,AE:ED=8:3,CD=16,则平行四边形ABCD的周长为
如图,平行四边ABCD中,BE平分∠ABC,AE:ED=8:3,CD=16,则平行四边形ABCD的周长为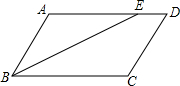 如图,平行四边ABCD中,BE平分∠ABC,AE:ED=8:3,CD=16,则平行四边形ABCD的周长为________.
如图,平行四边ABCD中,BE平分∠ABC,AE:ED=8:3,CD=16,则平行四边形ABCD的周长为________.