题目内容
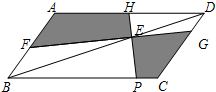 (2013•南京二模)如图,在?ABCD中,E是对角线BD上一点,过E点的线段FG、HP分别交平行四边形四边于F、G、H、P.若要使得图中两个阴影部分面积的大小关系是唯一确定的,则需要添加的条件是( )
(2013•南京二模)如图,在?ABCD中,E是对角线BD上一点,过E点的线段FG、HP分别交平行四边形四边于F、G、H、P.若要使得图中两个阴影部分面积的大小关系是唯一确定的,则需要添加的条件是( )分析:当FG∥BC,HP∥AB时,得出四边形EFBP和四边形DHEG是平行四边形,进而得出S四边形AFEH=S△ABD-S△BFE-S△DHE,S四边形EPCG=S△BCD-S△BEP-S△DEG,即可得出答案.
解答: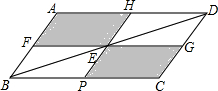 解:当FG∥BC,HP∥AB时,图中两个阴影部分面积的大小关系是唯一确定的.
解:当FG∥BC,HP∥AB时,图中两个阴影部分面积的大小关系是唯一确定的.
理由:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,AD∥BC,
∵AB∥PH,EF∥AD,
∴AD∥FG∥BC,AB∥HG∥CD,
∴∠ADB=∠DBC,四边形EFBP和四边形DHEG是平行四边形,
∵在△DAB和△BCD中
,
∴△DAB≌△BCD(AAS),
∴S△DAB=S△BCD,
同理S△DHE=S△DEG,S△EFB=S△BPE,
∵S四边形AFEH=S△ABD-S△BFE-S△DHE,S四边形EPCG=S△BCD-S△BEP-S△DEG,
∴S四边形AFEH=S四边形EPCG
∴当FG∥BC,HP∥AB时,图中两个阴影部分面积的大小关系是唯一确定的.
故选:C.
 解:当FG∥BC,HP∥AB时,图中两个阴影部分面积的大小关系是唯一确定的.
解:当FG∥BC,HP∥AB时,图中两个阴影部分面积的大小关系是唯一确定的.理由:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,AD∥BC,
∵AB∥PH,EF∥AD,
∴AD∥FG∥BC,AB∥HG∥CD,
∴∠ADB=∠DBC,四边形EFBP和四边形DHEG是平行四边形,
∵在△DAB和△BCD中
|
∴△DAB≌△BCD(AAS),
∴S△DAB=S△BCD,
同理S△DHE=S△DEG,S△EFB=S△BPE,
∵S四边形AFEH=S△ABD-S△BFE-S△DHE,S四边形EPCG=S△BCD-S△BEP-S△DEG,
∴S四边形AFEH=S四边形EPCG
∴当FG∥BC,HP∥AB时,图中两个阴影部分面积的大小关系是唯一确定的.
故选:C.
点评:本题考查了平行四边形的性质和判定,三角形的面积的应用,注意:平行四边形的性质是:①平行四边形的对边平行且相等,②平行四边形的对角相等,③平行四边形的对角线互相平分.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目