题目内容
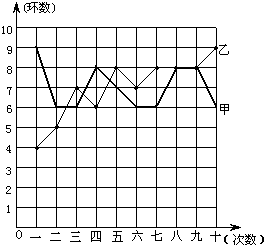 射击集训队在一个月的集训中,对甲、乙两名运动员进行了10次测试,成绩如图(折线图中,粗线表示甲,细线表示乙):
射击集训队在一个月的集训中,对甲、乙两名运动员进行了10次测试,成绩如图(折线图中,粗线表示甲,细线表示乙):(1)根据图中所提供的信息填写下表:
(2)请从下列四个不同的角度对测试结果进行分析:
①从平均数和方差结合谁的成绩好些?
②从平均数和众数结合谁的成绩好些?
③从折线图上两人射击环数的走势分析谁更有潜力.
④如果你是教练,会选择哪位运动员参加比赛?说明理由.
| 平均数 | 众数 | 方差 | |
| 甲 | 7 | 6 6 |
1.2 1.2 |
| 乙 | 7 7 |
8 8 |
2.2 |
分析:(1)结合折线统计图给出的数据,根据平均数、众数和方差的定义,进行计算填表;
(2)结合平均数、众数和方差三个方面分别进行分析,即可得出答案.
(2)结合平均数、众数和方差三个方面分别进行分析,即可得出答案.
解答:解:(1)乙的平均数是:(4+5+7+6+8+7+8+8+8+9)÷10=7,
甲中6出现了5次,出现的次数最多,则众数是6;乙中8出现了4次,出现的次数最多,众数是8;
甲的方差是:
[(9-7)2+5(6-7)2+3×(8-7)2+(7-7)2]=1.2;
填表如下:
故答案为:7,6,8,1.2;
(2)①从平均数看,两队的平均分相同,实力大体相当,但从方差看,甲队的成绩比较稳定,应选甲;
②从平均数上来看,甲与乙是一样的,从众数来看,乙的成绩好些;
③从折线图上两人射击环数的走势分析看,乙的波动小,乙更有潜力;
④如果我是教练,会选择乙运动员参加比赛,因为乙运动员的成绩呈上升趋势.
甲中6出现了5次,出现的次数最多,则众数是6;乙中8出现了4次,出现的次数最多,众数是8;
甲的方差是:
| 1 |
| 10 |
填表如下:
| 平均数 | 众数 | 方差 | |
| 甲 | 7 | 6 | 1.2 |
| 乙 | 7 | 8 | 2.2 |
(2)①从平均数看,两队的平均分相同,实力大体相当,但从方差看,甲队的成绩比较稳定,应选甲;
②从平均数上来看,甲与乙是一样的,从众数来看,乙的成绩好些;
③从折线图上两人射击环数的走势分析看,乙的波动小,乙更有潜力;
④如果我是教练,会选择乙运动员参加比赛,因为乙运动员的成绩呈上升趋势.
点评:本题考查了折线统计图、方差、平均数、众数的意义,方差反映数据的波动,平均数反映数据的平均水平,众数表示数据的集中程度.熟练掌握平均数的计算,理解众数和方差的概念是本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
为迎接“城运会”,某射击集训队在一个月的集训中,对甲、乙两名运动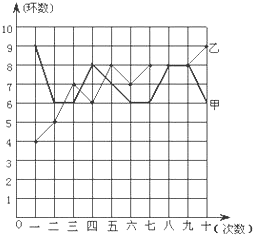 员进行了10次测试,成绩如图所示:
员进行了10次测试,成绩如图所示:
(1)根据下图所提供的信息完成表格:
(2)如果你是教练,会选择哪位运动员参加比赛?请说明理由.
 员进行了10次测试,成绩如图所示:
员进行了10次测试,成绩如图所示:(1)根据下图所提供的信息完成表格:
| 平均数 | 众数 | 方差 | |
| 甲 | 7 | 1.2 | |
| 乙 | 2.2 |
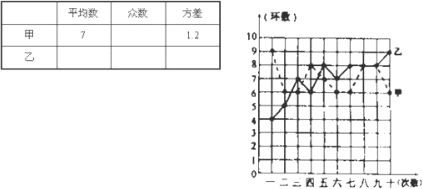
 射击集训队在一个月的集训中,对甲、乙两名运动员进行了10次测试,成绩如下:
射击集训队在一个月的集训中,对甲、乙两名运动员进行了10次测试,成绩如下: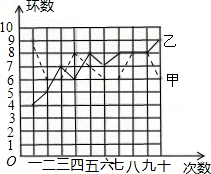 射击集训队在一个月的集训中,对甲、乙两名运动员进行了10次测试,
射击集训队在一个月的集训中,对甲、乙两名运动员进行了10次测试,