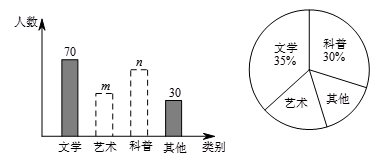
题目内容
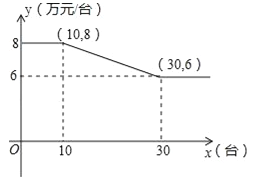
【题目】某公司销售智能机器人,售价每台为10万元,进价y与销售量x的函数关系式如图所示.
(1)当x=10时,公司销售机器人的总利润为 万元;
(2)当10≤x≤30时,求出y与x的函数关系式;
(3)问:销售量为多少台时,公司销售机器人的总利润为37.5万元.
【答案】(1)20;(2)![]() ;(3)15.
;(3)15.
【解析】
试题分析:(1)由“总利润=单台利润×销售数量”结合图象即可得出结论;
(2)设y与x之间的函数关系式为y=kx+b,由函数图象找出点的坐标,再利用待定系数法即可求出结论;
(3)设销售量为m台时,公司销售机器人的总利润为37.5万元.分析销售利润为37.5万元时,销售台数m的范围,再结合此时进价y与x的函数关系式得出销售m台时的进价,再由“总利润=单台利润×销售数量”即可得出关于m的一元二次方程,解方程即可得出结论..
试题解析:(1)当x=10时,公司销售机器人的总利润为10×(10﹣8)=20(万元).
故答案为:20.
(2)设y与x之间的函数关系式为y=kx+b,∵函数图象过点(10,8),(30,6),∴有![]() ,解得:
,解得: ,∴当10≤x≤30时,y与x的函数关系式为
,∴当10≤x≤30时,y与x的函数关系式为![]() .
.
(3)设销售量为m台时,公司销售机器人的总利润为37.5万元.
∵37.5>20,∴m>10,又∵m为正整数,∴4m≠37.5,∴只有在10<m<30内,公式销售机器人的总利润才有可能为37.5万元.
依题意得:m[10﹣(![]() )]=37.5,解得:m1=15,m2=﹣25(舍去).
)]=37.5,解得:m1=15,m2=﹣25(舍去).
答:销售量为15台时,公司销售机器人的总利润为37.5万元.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去租用这两种货车情况如下:
第一次 | 第二次 | |
甲种货车数量 | 2辆 | 5辆 |
乙种货车数量 | 3辆 | 6辆 |
累计运货重量 | 14吨 | 32吨 |
(1)分别求甲、乙两种货车载重多少吨?
(2)现在租用该公司5辆甲货车和7辆乙货车一次刚好运完这批货物,如果按每吨付费50元计算,货主应付运费多少元?