Question

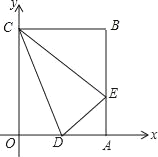
【题目】如图，在等腰△ABC中，AC＝BC，D在BC上，P是射线AD上一动点．

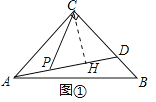
（1）如图①，若∠ACB＝90°，AC＝8，CD＝6，当点P在线段AD上，且△PCD是等腰三角形时，求AP长．

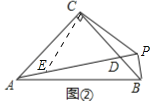
（2）如图②，若∠ACB＝90°，∠APC＝45°，当点P在AD延长线上时，探究PA，PB，PC的数量关系，并说明理由．

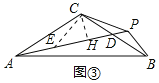
（3）类比探究：如图③，若∠ACB＝120°，∠APC＝30°，当点P在AD延长线上时，请直接写出表示PA，PB，PC的数量关系的等式．

Answer 1

【答案】（1）满足条件的AP的值为2.8或4或5；（2）PA﹣PB＝PC．理由见解析；（3）PA﹣PB＝PC．理由见解析.

【解析】

（1）如图①中，作CH⊥AD于H．利用面积法求出CH，利用勾股定理求出DH，再求出PD，接下来分三种情形解决问题即可；

（2）结论：PA﹣PB＝PC．如图②中，作EC⊥PC交AP于E．只要证明△ACE≌△BCP即可解决问题；

（3）结论：PA﹣PB＝PC．如图③中，在AP上取一点E，使得∠ECP＝∠ACB＝120°．只要证明△ACE≌△BCP即可解决问题；

（1）如图①中，作CH⊥AD于H．

在Rt△ACD中，AD＝＝10，

∵×AC×DC＝×AD×CH，

∴CH＝，

∴DH＝＝，

①当CP＝CD，∵CH⊥PD，

∴PH＝DH＝，

∴PD＝，

∴PA＝AD﹣PD＝10﹣＝．

②当CD＝DP时，DP＝6．AP＝10﹣6＝4，

③当CP＝PD时，易证AP＝PD＝5，

综上所述，满足条件的AP的值为2.8或4或5．

（2）结论：PA﹣PB＝PC．

理由：如图②中，作EC⊥PC交AP于E．

∵∠PCE＝90°，∠CPE＝45°，

∴∠CEP＝∠CPE＝45°，

∴CE＝CP，PE＝PC，

∵∠ACB＝∠ECP＝90°，

∴∠ACE＝∠BCP，

∵CA＝CB，

∴△ACE≌△BCP，

∴AE＝PB，

∴PA﹣PB＝PA﹣EA＝PE＝PC，

∴PA﹣PB＝PC．

（3）结论：PA﹣PB＝PC．

理由：如图③中，在AP上取一点E，使得∠ECP＝∠ACB＝120°．

∵∠CEP＝180°﹣120°﹣30°＝30°，

∴∠CEP＝∠CPE，

∴CE＝CP．作CH⊥PE于H，则PE＝PC，

∵∠ACB＝∠ECP，

∴∠ACE＝∠BCP，

∵CA＝CB，

∴△ACE≌△BCP，

∴AE＝PB，

∴PA﹣PB＝PA﹣EA＝PE＝PC．