题目内容
【题目】在平面直角坐标系xOy中,直线y=kx+4(k≠0)与y轴交于点A.
(1)如图,直线y=﹣2x+1与直线y=kx+4(k≠0)交于点B,与y轴交于点C,点B的横坐标为﹣1. ①求点B的坐标及k的值;
②直线y=﹣2x+1与直线y=kx+4与y轴所围成的△ABC的面积等于;
(2)直线y=kx+4(k≠0)与x轴交于点E(x0 , 0),若﹣2<x0<﹣1,求k的取值范围.
【答案】
(1)![]()
(2)解:∵直线y=kx+4(k≠0)与x轴交于点E(x0,0),﹣2<x0<﹣1,
∴当x0=﹣2,则E(﹣2,0),代入y=kx+4得:0=﹣2k+4,
解得:k=2,
当x0=﹣1,则E(﹣1,0),代入y=kx+4得:0=﹣k+4,
解得:k=4,
故k的取值范围是:2<k<4.
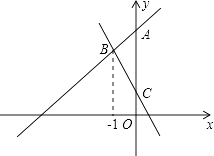
【解析】解:(1)①∵直线y=﹣2x+1过点B,点B的横坐标为﹣1, ∴y=2+1=3,
∴B(﹣1,3),
∵直线y=kx+4过B点,
∴3=﹣k+4,
解得:k=1;
②∵k=1,
∴一次函数解析式为:y=x+4,
∴A(0,4),
∵y=﹣2x+1,
∴C(0,1),
∴AC=4﹣1=3,
∴△ABC的面积为: ![]() ×1×3=
×1×3= ![]() ;
;
所以答案是: ![]() ;
;

练习册系列答案
相关题目