题目内容
【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利30元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.
(1)若商场平均每天赢利750元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天赢利最多?
【答案】(1)为了尽快减少库存,应减价15元;(2)降价10元时,利润最大为800元.
【解析】试题分析:(1)每天盈利=每件盈利×销售件数,每件实际盈利=原每件盈利-每件降价数.检验时,要考虑尽快减少库存,就是要保证盈利不变的情况下,降价越多,销售量越多,达到减少库存的目的.
(2)在(1)的基础上,由特殊到一般,列出二次函数,求出二次函数的最大值.
试题解析:解:(1)设每件衬衫应降价x元,依题意得:
(20+2x)(30-x)=750
解得:x=15或x=5.
为了尽快减少库存,应减价15元;
答:每件衬衫应降价15元.
(2)设平均每天盈利为P元,得:
P=(20+2x)(30-x) =-2x2+40x+600=![]()
∴当x=10时,P最大,最大值为800.
答:每件衬衫降价10元时,商场平均每天赢利最多.

【题目】如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定:
坡度 | 1:20 | 1:16 | 1:12 |
最大高度(米) | 1.50 | 1.00 | 0.75 |
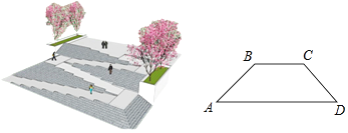
(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;
(2)求斜坡底部点A与台阶底部点D的水平距离AD.