ΧβΡΩΡΎ»ί
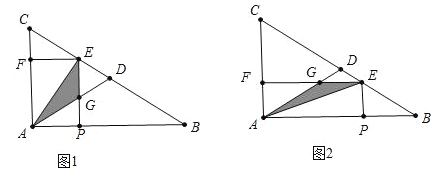
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœBAC=90ΓψΘ§AB=4Θ§AC=3Θ§ΒψDΈΣBCΒΡ÷–ΒψΘ§Ε·ΒψP¥”ΒψA≥ωΖΔΘ§“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―ΊœΏΕΈABœρΒψB‘ΥΕ·Θ§Β±ΒψPάκΩΣΒψAΚσΘ§ΙΐΒψPΉςPEΓΆABΫΜBC”ΎΒψEΘ§ΙΐΒψEΉςEFΓΆAC”ΎFΘ§…ηΒψP‘ΥΕ· ±ΦδΈΣtΘ®ΟκΘ©Θ§ΨΊ–ΈPEFA”κΓςADE÷ΊΒΰ≤ΩΖ÷ΒΡΟφΜΐΈΣSΤΫΖΫΒΞΈΜ≥ΛΕ»Θ°
Θ®1Θ©PEΒΡ≥ΛΈΣ Θ®”ΟΚ§tΒΡ¥ζ ΐ Ϋ±μ ΨΘ©ΘΜ
Θ®2Θ©«σS”κt÷°ΦδΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®3Θ©«σSΒΡΉν¥σ÷ΒΦΑS»ΓΒΟΉν¥σ÷Β ±tΒΡ÷ΒΘΜ
Θ®4Θ©Β±SΈΣΓςABCΟφΜΐΒΡ![]() ±Θ§tΒΡ÷Β”– ΗωΘ°
±Θ§tΒΡ÷Β”– ΗωΘ°
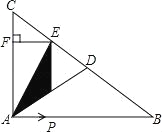
ΓΨ¥πΑΗΓΩ(1) ![]() Θ®4-tΘ©Θ°(2) S=
Θ®4-tΘ©Θ°(2) S=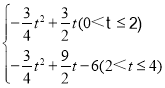 Θ°(3)
Θ°(3) ![]() Θ°(4)4.
Θ°(4)4.
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΗυΨίEPΓΈACΘ§ΒΟ![]() Θ§Ν–≥ω±»άΐ ΫΦ¥Ω…ΫβΨωΘ°
Θ§Ν–≥ω±»άΐ ΫΦ¥Ω…ΫβΨωΘ°
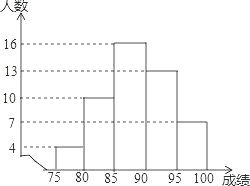
Θ®2Θ©Ζ÷ΝΫ÷÷«ι–ΈΧ÷¬έΔΌ»γΆΦ1÷–Θ§Β±0ΘΦtΓή2 ±Θ§ΗυΨίS=![]() EGAPΦ¥Ω…ΦΤΥψΘ§ΔΎ»γΆΦ2÷–Θ§Β±2ΘΦtΓή4 ±Θ§ΗυΨίS=
EGAPΦ¥Ω…ΦΤΥψΘ§ΔΎ»γΆΦ2÷–Θ§Β±2ΘΦtΓή4 ±Θ§ΗυΨίS=![]() GEAFΦ¥Ω…ΦΤΥψΘ°
GEAFΦ¥Ω…ΦΤΥψΘ°
Θ®3Θ©Ζ÷ΝΫ÷÷«ι–ΈΘ§άϊ”Ο≈δΖΫΖ®ΗυΨίΕΰ¥ΈΚ· ΐ–‘÷ Φ¥Ω…ΫβΨωΘ°
Θ®4Θ©Ζ÷ΝΫ÷÷«ι–ΈΘ§Ν–≥ωΖΫ≥ΧΦ¥Ω…ΫβΨωΘ§ΉΔ“βΦλ―ι «ΖώΖϊΚœΧβ“βΘ°
‘ΧβΫβΈωΘΚΘ®1Θ©»γΆΦ1÷–Θ§ΓΏEPΓΈACΘ§
Γύ![]() Θ§
Θ§
Γύ![]() ,
,
ΓύPE=![]() Θ®4-tΘ©Θ°
Θ®4-tΘ©Θ°
Θ®2Θ©ΔΌΒ±0ΘΦtΓή2 ±Θ§
ΓΏΓœBAC=90ΓψΘ§CD=DBΘ§
ΓύΓœDAB=ΓœBΘ§ΓΏΓœAPG=ΓœBAC=90ΓψΘ§
ΓύΓςAPGΓΉΓςBACΘ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύPG=![]() tΘ§
tȧ
ΓύEG=3-![]() tΘ§
tȧ
ΓύS=![]() EGAP=-
EGAP=-![]() t2+
t2+![]() tΘ°
tΘ°
ΔΎΒ±2ΘΦtΓή4 ±»γΆΦ2÷–Θ§ΓΏΓœFAG=ΓœCΘ§ΓœAFG=ΓœBACΘ§
ΓύΓςAFGΓΉΓςCABΘ§
Γύ![]() Θ§
Θ§
ΓύFG=4-tΘ§GE=2t-4Θ§
ΓύS=![]() GEAF=-
GEAF=-![]() t2+
t2+![]() -6Θ°
-6Θ°
Ήέ…œΥυ ωS=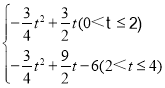 Θ°
Θ°
Θ®3Θ©Β±0ΘΦtΓή2 ±Θ§S=-![]() Θ®t-1Θ©2+
Θ®t-1Θ©2+![]() Θ§
Θ§
ΓΏ-![]() ΘΦ0Θ§
ΘΦ0Θ§
Γύt=1 ±Θ§SΉν¥σ÷ΒΈΣ![]() Θ§
Θ§
Β±2ΘΦtΓή4 ±Θ§S=-![]() Θ®t-3Θ©2+
Θ®t-3Θ©2+![]() Θ§
Θ§
ΓΏ-![]() ΘΦ0Θ§
ΘΦ0Θ§
Γύt=3 ±Θ§SΉν¥σ÷ΒΈΣ![]() Θ°
Θ°
Ήέ…œΥυ ωt=1Μρ3 ±Θ§SΉν¥σ÷ΒΕΦ «![]() Θ°
Θ°
Θ®4Θ©”…Χβ“β-![]() t2+
t2+![]() t=
t=![]() Θ§’ϊάμΒΟΒΫ5t2-10t+4=0Θ§t=
Θ§’ϊάμΒΟΒΫ5t2-10t+4=0Θ§t=![]() ΖϊΚœΧβ“βΘ°
ΖϊΚœΧβ“βΘ°
Μρ-![]() t2+
t2+![]() t-6=
t-6=![]() Θ§’ϊάμΒΟΒΫ5t2-30t+44=0Θ§t=
Θ§’ϊάμΒΟΒΫ5t2-30t+44=0Θ§t=![]() ΖϊΚœΧβ“βΘ§
ΖϊΚœΧβ“βΘ§
ΓύSΈΣΓςABCΟφΜΐΒΡ![]() ±Θ§tΒΡ÷Β”–ΥΡΗωΘ°
±Θ§tΒΡ÷Β”–ΥΡΗωΘ°