题目内容
(本题满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
直角三角板ABC中,∠A=30°,BC=1.将其绕直角顶点C逆时针旋转一个角![]() (
(![]() 且
且![]() ≠ 90°),得到Rt△
≠ 90°),得到Rt△![]() ,
,
(1)如图9,当![]() 边经过点B时,求旋转角
边经过点B时,求旋转角![]() 的度数;
的度数;
(2)在三角板旋转的过程中,边![]() 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥ 交
交![]() 边于点E,联结BE.
边于点E,联结BE.
①当![]() 时,设
时,设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数解析式及定义域;
之间的函数解析式及定义域;
②当![]() 时,求
时,求![]() 的长.
的长.


解:(1)在Rt△![]() 中,∵∠A=30°,
中,∵∠A=30°,
∴![]() .………………………………………………………(1分)
.………………………………………………………(1分)
由旋转可知:![]() ,
,![]() ,
,![]()
∴△![]() 为等边三角形.……………(2分)
为等边三角形.……………(2分)
∴![]() =
=![]() .……………(1分)
.……………(1分)
(2)①当![]() 时,点D在AB边上(如图).
时,点D在AB边上(如图).
∵DE∥![]() ,
,
∴ ![]() ..…………………………………………………(1分)
..…………………………………………………(1分)
由旋转性质可知,CA =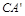 ,CB=
,CB=![]() ,∠ACD=∠BCE.
,∠ACD=∠BCE.
∴ ![]() ,.…………………………………………………(1分)
,.…………………………………………………(1分)
∴ ![]() .
.
∴ △CAD∽△CBE. .………………………………………(1分)
∴![]() .
.
∵∠A=30°
∴![]()
![]() .……………………………………………(1分)
.……………………………………………(1分)
∴![]() (0﹤
(0﹤![]() ﹤2)…………………………………………(2分)
﹤2)…………………………………………(2分)
②当![]() 时,点D在AB边上
时,点D在AB边上
AD=x,![]() ,∠DBE=90°.
,∠DBE=90°.
此时,![]() .
.
当S=![]() 时,
时,![]() .
.
整理,得 ![]() .
.
解得 ![]() ,即AD=1. …………………………………(2分)
,即AD=1. …………………………………(2分)
当![]() 时,点D在AB的延长线上(如图)
时,点D在AB的延长线上(如图)
.
仍设AD=x,则![]() ,∠DBE=90°..
,∠DBE=90°..
![]() .
.
当S=![]() 时,
时,![]() .
.
整理,得 ![]() .
.
解得 ![]() ,
,![]() (负值,舍去).
(负值,舍去).
即![]() .…………………………………………………(2分)
.…………………………………………………(2分)
综上所述:AD=1或![]() .
.
解析:略

练习册系列答案
相关题目
 满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分) (
( 且
且 ,
, 边经过点B时,求旋转角
边经过点B时,求旋转角 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥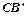 边于点E,联结BE.
边于点E,联结BE. 时,设
时,设 ,
,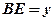 ,求
,求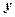 与
与 之间的函数解析式及定义域;
之间的函数解析式及定义域; 时,求
时,求 的长.
的长. 

 .
. 、E分别与△ENB的顶点E、N、B对应),求AP的
、E分别与△ENB的顶点E、N、B对应),求AP的 长.
长.
 .
.
