题目内容
(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)在Rt△ABC中,∠ACB=90°,BC=30,AB=50.点P是AB边上任意一点,直线PE⊥AB,与边AC或BC相交于E.点M在线段AP上,点N在线段BP上,EM=EN, .
.
(1)如图1,当点E与点C重合时,求CM的长;
(2)如图2,当点E在边AC上时,点E不与点A、C重合,设AP=x,BN=y,求y关于x的函数关系式,并写出函数的定义域;
(3)若△AME∽△ENB(△AME的顶点A、M、E分别与△ENB的顶点E、N、B对应),求AP的长.

(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)
[解] (1) 由AE=40,BC=30,AB=50,ÞCP=24,又sinÐEMP=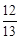 ÞCM=26。
ÞCM=26。
(2) 在Rt△AEP與Rt△ABC中,∵ ÐEAP=ÐBAC,∴ Rt△AEP ~ Rt△ABC,
∴ 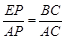 ,即
,即 ,∴ EP=
,∴ EP= x,
x,
又sinÐEMP=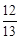 ÞtgÐEMP=
ÞtgÐEMP= =
=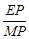 Þ
Þ =
= ,∴ MP=
,∴ MP=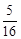 x=PN,
x=PN,
BN=AB-AP-PN=50-x-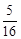 x=50-
x=50-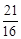 x
(0<x<32)。
x
(0<x<32)。
(3) j 當E在線段AC上時,由(2)知, ,即
,即 ,ÞEM=
,ÞEM=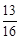 x=EN,
x=EN,
又AM=AP-MP=x-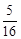 x=
x= x,
x,
由題設△AME ~ △ENB,∴ 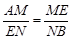 ,Þ
,Þ =
=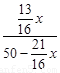 ,解得x=22=AP。
,解得x=22=AP。
k 當E在線段BC上時,由題設△AME ~ △ENB,∴ ÐAEM=ÐEBN。
由外角定理,ÐAEC=ÐEAB+ÐEBN=ÐEAB+ÐAEM=ÐEMP,
∴ Rt△ACE ~ Rt△EPM,Þ ,即
,即 ,ÞCE=
,ÞCE= …j。
…j。
設AP=z,∴PB=50-z,
由Rt△BEP ~ Rt△BAC,Þ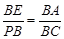 ,即
,即 =
= ,ÞBE=
,ÞBE=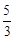 (50-z),∴CE=BC-BE=30-
(50-z),∴CE=BC-BE=30-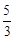 (50-z)…k。
(50-z)…k。
由j,k,解 =30-
=30-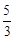 (50-z),得z=42=AP。
(50-z),得z=42=AP。
【解析】略

 交
交

 满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分) (
( 且
且 ,
, 边经过点B时,求旋转角
边经过点B时,求旋转角 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥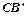 边于点E,联结BE.
边于点E,联结BE. 时,设
时,设 ,
,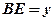 ,求
,求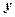 与
与 之间的函数解析式及定义域;
之间的函数解析式及定义域; 时,求
时,求 的长.
的长. 

 .
. 、E分别与△ENB的顶点E、N、B对应),求AP的
、E分别与△ENB的顶点E、N、B对应),求AP的 长.
长.
