题目内容
对于每个x，函数y是y1=2x，y2=x+2，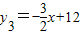
这三个函数中的最小值，则函数y的最大值是（ ）A．4
B．6
C．8
D．
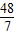
【答案】分析：分别联立三个函数中任意两函数，求出函数的交点坐标，根据此交点坐标即可求解．
解答：解：分别联立y1、y2，y1、y3，y2、y3，
可知y1、y2的交点A（2，4）；y1、y3的交点B（
，
）；y2、y3的交点C（4，6），
∴当x≤2时，y最小=4；
当2＜x≤
时，y最小=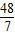
；
当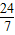
＜x≤4时，y最小=6；
当x＞4时，y最小＞6．
故选B．
点评：本题考查的是一次函数的性质，根据题意得出任意两函数的交点坐标是解答此题的关键．
解答：解：分别联立y1、y2，y1、y3，y2、y3，
可知y1、y2的交点A（2，4）；y1、y3的交点B（
，）；y2、y3的交点C（4，6），∴当x≤2时，y最小=4；
当2＜x≤
时，y最小=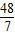；当
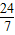＜x≤4时，y最小=6；当x＞4时，y最小＞6．
故选B．
点评：本题考查的是一次函数的性质，根据题意得出任意两函数的交点坐标是解答此题的关键．
练习册系列答案
相关题目