题目内容
对于每个x，函数y是y1=-x+6，y2=-2x2+4x+6这两个函数的较小值，则函数y的最大值是 ．
【答案】分析：根据函数解析式，在同一平面直角坐标系内作出大致图象，然后根据图象即可解答．
解答：
解：函数y1=-x+6，y2=-2x2+4x+6的图象如图，
x＜0时，函数y的最大值是6，
x＞0时，函数y的最大值不论在y=-x+6上取得，还是在y2=-2x2+4x+6取得，总有y＜6，
∴函数y的最大值是6．
故答案为：6．
点评：本题考查了二次函数的最值问题，作出图象，利用数形结合的思想求解更加简便．
解答：
解：函数y1=-x+6，y2=-2x2+4x+6的图象如图，x＜0时，函数y的最大值是6，
x＞0时，函数y的最大值不论在y=-x+6上取得，还是在y2=-2x2+4x+6取得，总有y＜6，
∴函数y的最大值是6．
故答案为：6．
点评：本题考查了二次函数的最值问题，作出图象，利用数形结合的思想求解更加简便．
练习册系列答案
阅读快车系列答案
相关题目
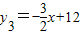这三个函数中的最小值，则函数y的最大值是（ ）