题目内容
(2009•同安区模拟)若关于x的一元二次方程x2+(m+1)x+
m2=0有两个不相等的实数根,则m的取值范围是
| 1 |
| 4 |
m>-
| 1 |
| 2 |
m>-
.| 1 |
| 2 |
分析:根据一元二次方程的根的判别式,建立关于m的不等式,求出m的取值范围.
解答:解:因为关于x的一元二次方程x2+(m+1)x+
m2=0有两个不相等的实数根.
所以△=(m+1)2-4×
m2>0
解之得m>-
.
故答案为m>-
.
| 1 |
| 4 |
所以△=(m+1)2-4×
| 1 |
| 4 |
解之得m>-
| 1 |
| 2 |
故答案为m>-
| 1 |
| 2 |
点评:本题考查了一元二次方程根的判别式的应用.
总结:一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
总结:一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 (2009•同安区模拟)已知:如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点P,过点P作⊙O的切线PD交AC于D.
(2009•同安区模拟)已知:如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点P,过点P作⊙O的切线PD交AC于D.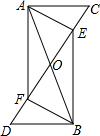 (2009•同安区模拟)已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.
(2009•同安区模拟)已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.