题目内容
(2009•同安区模拟)(1)先化简,再求值
•
,其中x=3
(2)6sin45°-(2)0-
(3)解方程x2+2x-2=0.
| x2+x |
| x2 |
| x |
| x2-1 |
(2)6sin45°-(2)0-
| 18 |
(3)解方程x2+2x-2=0.
分析:(1)先对分子与分母分解因式,再约分,代入x的值进行计算即可;
(2)根据特殊角的三角函数值、零指数幂、二次根式的化简进行计算即可;
(3)用配方法解方程即可.
(2)根据特殊角的三角函数值、零指数幂、二次根式的化简进行计算即可;
(3)用配方法解方程即可.
解答:解:(1)原式=
•
=
,
当x=3时,原式=
=
;
(2)原式=6×
-1-3
=3
-1-3
=-1;
(3)移项得,x2+2x=2,
x2+2x+1=2+1,
(x+1)2=3,
即x+1=±
,
x1=
-1,x2=-
-1.
| x(x+1) |
| x2 |
| x |
| (x+1)(x-1) |
=
| 1 |
| x-1 |
当x=3时,原式=
| 1 |
| 3-1 |
| 1 |
| 2 |
(2)原式=6×
| ||
| 2 |
| 2 |
=3
| 3 |
| 2 |
=-1;
(3)移项得,x2+2x=2,
x2+2x+1=2+1,
(x+1)2=3,
即x+1=±
| 3 |
x1=
| 3 |
| 3 |
点评:本题考查了分式的化简求值,二次根式的求值与化简以及解一元二次方程,此题是基础知识要熟练掌握.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 (2009•同安区模拟)已知:如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点P,过点P作⊙O的切线PD交AC于D.
(2009•同安区模拟)已知:如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点P,过点P作⊙O的切线PD交AC于D.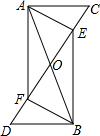 (2009•同安区模拟)已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.
(2009•同安区模拟)已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.