题目内容
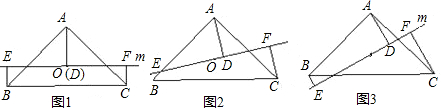
探究问题:已知AD、BE分别为△ABC 的边BC、AC上的中线,且AD、BE交于点O.
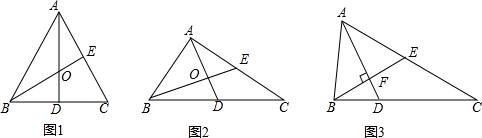
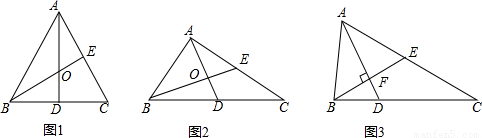
(1)△ABC为等边三角形,如图1,则AO:OD=______;
(2)当小明做完(1)问后继续探究发现,若△ABC为一般三角形(如图2),(1)中的结论仍成立,请你给予证明.
(3)运用上述探究的结果,解决下列问题:
如图3,在△ABC中,点E是边AC的中点,AD平分∠BAC,AD⊥BE于点F,若AD=BE=4.求:△ABC的周长.
【答案】分析:(1)连接DE,由三角形中位线性质,即可得DE∥AB,DE= AB,则可证得△ODE∽△OAB,然后由相似三角形的对应边成比例,即可求得AO:OD的值;
AB,则可证得△ODE∽△OAB,然后由相似三角形的对应边成比例,即可求得AO:OD的值;
(2)同(1),连接DE,由三角形中位线性质,即可得DE∥AB,DE= AB,则可证得△ODE∽△OAB,然后由相似三角形的对应边成比例,即可求得AO:OD的值;
AB,则可证得△ODE∽△OAB,然后由相似三角形的对应边成比例,即可求得AO:OD的值;
(3)过点C作CG∥BE,交AB延长线于点G,并延长AD交CG于点H,易证得△ABE与△ACG是等腰三角形,利用(2)的结论与勾股定理,即可求得AB、BC、AC的长.
解答:(1)解:连接DE,
∵AD、BE分别为△ABC的边BC、AC上的中线,
∴DE∥AB,DE= AB,
AB,
∴△ODE∽△OAB,
∴AO:OD=AB:DE=2:1.
故答案为:2:1;
(2)证明:连接DE,
∵D、E为AC、BC中点,
∴DE∥AB,DE= AB,
AB,
∴△DOE∽△AOB,
∴AO:OD=AB:DE=2:1.
(3)解:过点C作CG∥BE,交AB延长线于点G,并延长AD交CG于点H.
∵E是边AC的中点,
∴B是边AG的中点,
∴BE是△ACG中位线,
∵AD平分∠BAC,AD⊥BE于点F,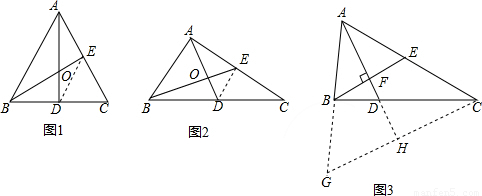
∴∠BAF=∠EAF,∠AFB=∠AFE=90°,
在△ABF和△AEF中,
∵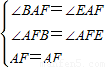 ,
,
∴△ABF≌△AEF(AAS),
∴AB=AE,
∵BE∥CG,
∴AB:AG=AE:AC,
∴AG=AC,
∵AF⊥BE,
∴AH⊥CG,
∴H为CG中点,
由上述结果可知:AD:DH=2:1,CD:DB=2:1,
∴DH= AD=
AD= ×4=2,
×4=2,
∴AH=AD+DH=6,
∵CG=2BE=8,
∴CH=GH=4,
∵BE为中位线,
∴AF=FH= AH=3,
AH=3,
∴DF=AD-AF=4-3=1,
在Rt△DHC中,CD=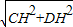 =
=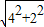 =2
=2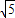 ,
,
∴BD= CD=
CD=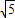 ,
,
∴BC=BD+CD=3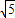 ,
,
在Rt△AHC中,AC=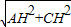 =
=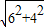 =2
=2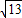 ,
,
∴AB= AG=
AG= AC=
AC=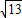 ,
,
∴△ABC周长为:AB+BC+AC=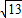 +3
+3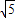 +2
+2 =3
=3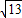 +3
+3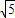 .
.
点评:此题考查了相似三角形的判定与性质、三角形的中位线的性质、全等三角形的判定与性质以及勾股定理等知识.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.
 AB,则可证得△ODE∽△OAB,然后由相似三角形的对应边成比例,即可求得AO:OD的值;
AB,则可证得△ODE∽△OAB,然后由相似三角形的对应边成比例,即可求得AO:OD的值;(2)同(1),连接DE,由三角形中位线性质,即可得DE∥AB,DE=
 AB,则可证得△ODE∽△OAB,然后由相似三角形的对应边成比例,即可求得AO:OD的值;
AB,则可证得△ODE∽△OAB,然后由相似三角形的对应边成比例,即可求得AO:OD的值;(3)过点C作CG∥BE,交AB延长线于点G,并延长AD交CG于点H,易证得△ABE与△ACG是等腰三角形,利用(2)的结论与勾股定理,即可求得AB、BC、AC的长.
解答:(1)解:连接DE,
∵AD、BE分别为△ABC的边BC、AC上的中线,
∴DE∥AB,DE=
 AB,
AB,∴△ODE∽△OAB,
∴AO:OD=AB:DE=2:1.
故答案为:2:1;
(2)证明:连接DE,
∵D、E为AC、BC中点,
∴DE∥AB,DE=
 AB,
AB,∴△DOE∽△AOB,
∴AO:OD=AB:DE=2:1.
(3)解:过点C作CG∥BE,交AB延长线于点G,并延长AD交CG于点H.
∵E是边AC的中点,
∴B是边AG的中点,
∴BE是△ACG中位线,
∵AD平分∠BAC,AD⊥BE于点F,

∴∠BAF=∠EAF,∠AFB=∠AFE=90°,
在△ABF和△AEF中,
∵
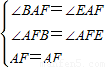 ,
,∴△ABF≌△AEF(AAS),
∴AB=AE,
∵BE∥CG,
∴AB:AG=AE:AC,
∴AG=AC,
∵AF⊥BE,
∴AH⊥CG,
∴H为CG中点,
由上述结果可知:AD:DH=2:1,CD:DB=2:1,
∴DH=
 AD=
AD= ×4=2,
×4=2,∴AH=AD+DH=6,
∵CG=2BE=8,
∴CH=GH=4,
∵BE为中位线,
∴AF=FH=
 AH=3,
AH=3,∴DF=AD-AF=4-3=1,
在Rt△DHC中,CD=
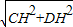 =
=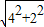 =2
=2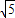 ,
,∴BD=
 CD=
CD=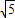 ,
,∴BC=BD+CD=3
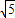 ,
,在Rt△AHC中,AC=
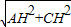 =
=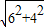 =2
=2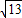 ,
,∴AB=
 AG=
AG= AC=
AC=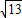 ,
,∴△ABC周长为:AB+BC+AC=
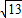 +3
+3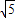 +2
+2 =3
=3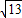 +3
+3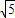 .
.点评:此题考查了相似三角形的判定与性质、三角形的中位线的性质、全等三角形的判定与性质以及勾股定理等知识.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 20、问题:已知△ABC中,∠BAC=2∠ACB,点D是△ABC内的一点,且AD=CD,BD=BA.探究∠DBC与∠ABC度数的比值.
20、问题:已知△ABC中,∠BAC=2∠ACB,点D是△ABC内的一点,且AD=CD,BD=BA.探究∠DBC与∠ABC度数的比值.