题目内容
某中学八年(1)班利用70元钱的班费,同时购买单价分别为3元、2元、1元的甲、乙、丙三种纪念品,奖励参加校“元旦会演”活动的同学。已知购买乙种纪念品件数比购买甲种纪念品的件数多2件,而购买甲种纪念品的件数不少于10件,且购买甲种纪念品的费用不超过总费用的一半,若购买的甲、乙、丙三种纪念品恰好用了70元钱,问可有几种购买方案?每种方案中购买的甲、乙、丙三种纪念品各有多少件?
两种购买方案:购买甲、乙、丙纪念品分别为10、12、16件或11、13、11件。
试题分析:设购买甲纪念品为x元,则乙为(x+2)元,由于甲、乙、丙三种纪念品恰好用了70元钱,则买甲、乙两种纪念品的钱≤70,再根据甲种纪念品的件数不少于10件,且购买甲种纪念品的费用不超过总费用的一半,列不等式解答.
设买甲种纪念品数量为x,丙种纪念品数量为y,则乙种纪念品数量为(x+2),
则
 ,解得
,解得
又
 且
且
解得

∴x=10或11
∴可有两种购买方案:购买甲、乙、丙纪念品分别为10、12、16件或11、13、11件。
点评:解答本题的关键是将现实生活中的事件与数学思想联系起来,读懂题意,根据甲、乙、丙纪念品的数量及价格列出不等式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 >0,
>0, >0,有如下四个结论:
>0,有如下四个结论: >
> >
> >x
>x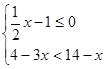 并将其解集在数轴上表示出来。
并将其解集在数轴上表示出来。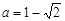 时,求
时,求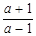 -
-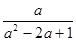 ÷
÷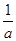 的值.
的值.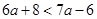 (2)
(2)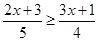
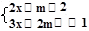 无解,则 m 的取值范围 .
无解,则 m 的取值范围 .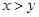 ,则下列不等式中成立的是( )
,则下列不等式中成立的是( )



 的解集为x>2,则a的取值范围为______
的解集为x>2,则a的取值范围为______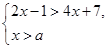 无解,则实数a的取值范围是( )
无解,则实数a的取值范围是( )