题目内容
如图，OB，OC是⊙O的半径，已知∠B=20°，∠C=30°，则∠BOC=
- A.50°
- B.80°
- C.100°
- D.130°
C
分析：连接AO，并延长，交圆于点E，则有∠BOC=∠BOE+∠COE=∠ABO+∠BAO+∠ACO+∠CAO=∠A+∠ABO+∠ACO，又根据圆周角定理可证2∠A=∠BOC，即可求∠A=50°，再根据圆周角定理即可得出∠BOC的度数．
解答：
解：连接AO，并延长，交圆于点E，
∴∠BOC=∠BOE+∠COE=∠ABO+∠BAO+∠ACO+∠CAO=∠A+∠ABO+∠ACO，
∵2∠A=∠BOC，
∴∠A=50°．
∴∠BOC=2∠A=100°．
故选C．
点评：本题考查的是圆周角定理，根据题意作出辅助线是解答此题的关键．
分析：连接AO，并延长，交圆于点E，则有∠BOC=∠BOE+∠COE=∠ABO+∠BAO+∠ACO+∠CAO=∠A+∠ABO+∠ACO，又根据圆周角定理可证2∠A=∠BOC，即可求∠A=50°，再根据圆周角定理即可得出∠BOC的度数．
解答：
解：连接AO，并延长，交圆于点E，∴∠BOC=∠BOE+∠COE=∠ABO+∠BAO+∠ACO+∠CAO=∠A+∠ABO+∠ACO，
∵2∠A=∠BOC，
∴∠A=50°．
∴∠BOC=2∠A=100°．
故选C．
点评：本题考查的是圆周角定理，根据题意作出辅助线是解答此题的关键．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
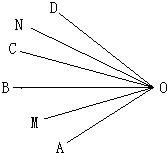16、如图，OB，OC是∠AOD的任意两条射线，OM平分∠AOB，ON平分∠COD，若∠MON=α，∠BOC=β，则表示∠AOD的代数式是∠AOD=
10、如图，OB、OC是∠ABC、∠ACB的角平分线，∠BOC=140°，则∠A等于（ ）
19、如图，OB、OC是⊙O的半径，A是⊙O上一点，若已知∠B=20°，∠C=30°，则∠A=
如图，OB、OC是⊙O的半径，A是⊙O上一点，若∠BOC=100°，则∠BAC等于（ ）
如图，OB，OC是⊙O的半径，已知∠B=20°，∠C=30°，则∠BOC=（ ）