题目内容
 如图,点O是AB上的一点,OC为任意一条射线,另有OD,OE分别平分∠AOC,∠BOC.
如图,点O是AB上的一点,OC为任意一条射线,另有OD,OE分别平分∠AOC,∠BOC.(1)已知∠AOC=40°,求∠DOE的度数;
(2)当∠BOC=110°时,∠DOE=
90°
90°
(填度数);(3)由(1)(2)的结果,你能得到什么结论?并说明理由.
分析:(1)根据平角定义得到∠AOB=180°,则可计算出∠BOC=140°,再根据角平分线的定义得到∠COD=
∠AOC=20°,∠COE=
∠BOC=70°,然后利用∠DOE=∠COD+∠COE进行计算;
(2)先计算出∠AOC=70°,再根据角平分线的定义得到∠COD=
∠AOC=35°,∠COE=
∠BOC=55°,然后利用∠DOE=∠COD+∠COE进行计算;
(3)根据平角定义得到∠AOB=180°,再根据角平分线的定义得到∠COD=
∠AOC,∠COE=
∠BOC,则∠DOE=∠COD+∠COE=
∠AOC+
∠BOC=
(∠AOC+∠BOC)=
∠AOB=90°.
| 1 |
| 2 |
| 1 |
| 2 |
(2)先计算出∠AOC=70°,再根据角平分线的定义得到∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
(3)根据平角定义得到∠AOB=180°,再根据角平分线的定义得到∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵点O是AB上的一点,
∴∠AOB=180°,
∴∠BOC=180°-40°=140°,
∵OD,OE分别平分∠AOC,∠BOC,
∴∠COD=
∠AOC=
×40°=20°,∠COE=
∠BOC=70°,
∴∠DOE=∠COD+∠COE=90°;
(2)∵∠BOC=110°,
∴∠AOC=180°-110°=70°,
∵OD,OE分别平分∠AOC,∠BOC,
∴∠COD=
∠AOC=
×70°=35°,∠COE=
∠BOC=55°,
∴∠DOE=∠COD+∠COE=90°;
故答案为90°;
(3)∠DOE的度数为90°.理由如下:
∵点O是AB上的一点,
∴∠AOB=180°,
∵OD,OE分别平分∠AOC,∠BOC,
∴∠COD=
∠AOC,∠COE=
∠BOC,
∴∠DOE=∠COD+∠COE=
∠AOC+
∠BOC=
(∠AOC+∠BOC)=
∠AOB=90°.
∴∠AOB=180°,
∴∠BOC=180°-40°=140°,
∵OD,OE分别平分∠AOC,∠BOC,
∴∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DOE=∠COD+∠COE=90°;
(2)∵∠BOC=110°,
∴∠AOC=180°-110°=70°,
∵OD,OE分别平分∠AOC,∠BOC,
∴∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DOE=∠COD+∠COE=90°;
故答案为90°;
(3)∠DOE的度数为90°.理由如下:
∵点O是AB上的一点,
∴∠AOB=180°,
∵OD,OE分别平分∠AOC,∠BOC,
∴∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DOE=∠COD+∠COE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了角度的计算:会计算角度的和、差、倍、分.也考查了角平分线的定义.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
 如图,点C是线段上的一点,点D,E分别是AC和CB 的中点,已知AB=15,则DE的长为
如图,点C是线段上的一点,点D,E分别是AC和CB 的中点,已知AB=15,则DE的长为 23、已知,如图,点C是AB上一点,分别以AC,BC为边,在AB的同侧作等边三角形△ACD和△BCE.
23、已知,如图,点C是AB上一点,分别以AC,BC为边,在AB的同侧作等边三角形△ACD和△BCE.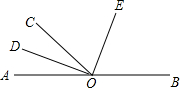 如图,点O是AB上的一点,OC为任意一条射线,另有OD,OE分别平分∠AOC,∠BOC.
如图,点O是AB上的一点,OC为任意一条射线,另有OD,OE分别平分∠AOC,∠BOC.