题目内容
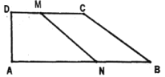
【题目】如图,AB∥CD,点A,E,B,C不在同一条直线上.

(1)如图1,求证:∠E+∠C﹣∠A=180°
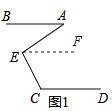
(2)如图2.直线FA,CP交于点P,且∠BAF=![]() ∠BAE,∠DCP=
∠BAE,∠DCP=![]() ∠DCE.
∠DCE.
①试探究∠E与∠P的数量关系;
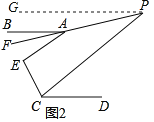
②如图3,延长CE交PA于点Q,若AE∥PC,∠BAQ=α(0°<α<22.5°),则∠PQC的度数为 (用含α的式子表示)
【答案】(1)详见解析;(2)①∠E=180°﹣3∠P,理由详见解析;②180°﹣8α
【解析】
(1)如图1,过E作EF∥AB,根据平行线的性质即可得到结论;
(2)①设∠BAF=x,∠BAE=3x,∠DCP=y,∠DCE=3y,由(1)知,∠E=180°﹣∠C+∠A=180°﹣3(y﹣x),如图2,过P作PG∥CD,根据平行线的性质即可得到结论;
②如图3,过P作PG∥CD,根据平行线的性质即可得到结论.
解:(1)如图1,过E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠AEF=∠A,∠C+∠FEC=180°,
∴∠E=∠AEF+∠FEC=∠A+180°﹣∠C,
即∠E+∠C﹣∠A=180°;
(2)①∵∠BAF=![]() ∠BAE,∠DCP=
∠BAE,∠DCP=![]() ∠DCE,
∠DCE,
∴设∠BAF=x,∠BAE=3x,∠DCP=y,∠DCE=3y,
由(1)知,∠E=180°﹣∠C+∠A=180°﹣3(y﹣x),
如图2,过P作PG∥CD,
∵AB∥CD,
∴AB∥PG,
∴∠GPA=∠BAF=x,∠GPC=∠PCD=y,
∴∠APC=y﹣x,
即∠E=180°﹣3∠P;
②如图3,过P作PG∥CD,
∵∠BAQ=α,
∴∠QAE=2α,
∵AE∥PC,
∴∠QAE=∠APC=2α,
由①知,∠AEC=180°﹣3∠APC=180°﹣6α,
∴∠PQC=∠AEC﹣∠QAE=180°﹣6α﹣2α=180°﹣8α,
故答案为:180°﹣8α.

 阅读快车系列答案
阅读快车系列答案