题目内容
若方程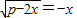
有两个不相等的实数根，则实数p的取值范围是（ ）A．p＞-1
B．p≤0
C．-1＜p≤0
D．-1≤p＜0
【答案】分析：通过平方有理化，将无理方程根的个数讨论转化为一元二次方程实根个数的讨论，但需注意注
的隐含制约．
解答：解：方程
，两边平方得：p-2x=x2，
∴x2+2x-p=0，
∵方程有两个不相等的实数根，
∴△=4+4p＞0，且x1+x2＜0，x1x2，≥0，
∴-1＜p≤0．
故选C．
点评：本题考查了无理方程，难度不大，关键是将无理方程根的个数讨论转化为一元二次方程实根个数的讨论；注：转化与化归是一种重要的数学思想，在数学学习与解数学题中，我们常常用到下列不同途径的转化：实际问题转化大为数学问题，数与形的转化，常量与变量的转化，一般与特殊的转化等．
的隐含制约．解答：解：方程
，两边平方得：p-2x=x2，∴x2+2x-p=0，
∵方程有两个不相等的实数根，
∴△=4+4p＞0，且x1+x2＜0，x1x2，≥0，
∴-1＜p≤0．
故选C．
点评：本题考查了无理方程，难度不大，关键是将无理方程根的个数讨论转化为一元二次方程实根个数的讨论；注：转化与化归是一种重要的数学思想，在数学学习与解数学题中，我们常常用到下列不同途径的转化：实际问题转化大为数学问题，数与形的转化，常量与变量的转化，一般与特殊的转化等．
练习册系列答案
相关题目