题目内容
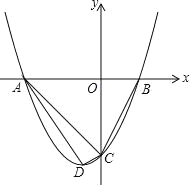
【题目】已知:二次函数y=ax2+bx+c的图象与x轴相交于A(-4,0),B(2,0)两点,与y轴相交于点C(0,-4),点D为抛物线的顶点.
(1)求二次函数的解析式;
(2)求S△ABC:S△ACD的值.
【答案】(1)抛物线解析式为y=![]() x2+x-4,(2)4:1.
x2+x-4,(2)4:1.
【解析】
试题分析:(1)设抛物线解析式为y=a(x+4)(x-2),把点C(0,-4)代入即可.
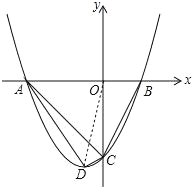
(2)连接OD,根据S△ADC=S△AOD+S△OCD-S△AOC求出△ADC面积即可解决问题.
试题解析:(1)∵二次函数y=ax2+bx+c的图象与x轴相交于A(-4,0),B(2,0)两点,
∴可以假设抛物线解析式为y=a(x+4)(x-2),
∵与y轴相交于点C(0,-4),
∴-4=-8a,
∴a=![]() ,
,
∴抛物线解析式为y=![]() x2+x-4,
x2+x-4,
(2)连接OD.
∵y=![]() x2+x-4=
x2+x-4=![]() (x+1)2-
(x+1)2-![]() ,
,
∴点D坐标(-1,-![]() ),
),
∴S△ABC=![]() ×AB×OC=
×AB×OC=![]() ×6×4=12,
×6×4=12,
S△ADC=S△AOD+S△OCD-S△AOC=![]() ×4×
×4×![]() +
+![]() ×4×1-
×4×1-![]() ×4×4=3.
×4×4=3.
∴S△ABC:S△ADC=12:3=4:1.

练习册系列答案
相关题目

