Question

圆O的半径为6cm，P是圆O内一点，OP=2cm，那么过点P的最短弦的长等于（　　）

• A、4

  2

  cm
• B、8

  2

  cm
• C、6

  2

  cm
• D、12cm

Answer 1

分析：过点P的最短弦是垂直于OP的弦CD．根据勾股定理和垂径定理求解．

解答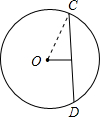：解：过点P的最短弦是垂直于OP的弦CD，
连接OC．根据勾股定理，得PC=

36-4

=4

2

，
再根据垂径定理，得CD=8

2

．
故选B．

点评：此题首先要能够正确作出过点P的最短的弦，然后综合运用垂径定理和勾股定理．