题目内容
在⊙O中,AB和CD是两条平行弦,AB、CD所对的圆心角分别为120°和60°,圆O的半径为6cm,则AB、CD之间的距离是
(3
+3)cm或(3
-3)cm
| 3 |
| 3 |
(3
+3)cm或(3
-3)cm
.| 3 |
| 3 |
分析:根据题意画出符合条件的两种情况,求出OE和OF的值,即可求出EF的长.
解答:解:分为两种情况:
①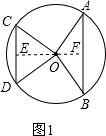 如图1,过O作OE⊥CD于E,延长EO交AB于F,
如图1,过O作OE⊥CD于E,延长EO交AB于F,
∵AB∥CD,
∴EF⊥AB,
∵CO=DO=6cm,∠COD=60°,
∴CE=DE=3cm,∠OE⊥CD,
∴在Rt△CEO中,由勾股定理得:EO=
=3
(cm),
∵AO=BO,∠AOB=120°,EF⊥AB,
 ∴∠A=∠B=30°,∠AFO=90°,
∴∠A=∠B=30°,∠AFO=90°,
∴OF=
AO=3cm,
∴EF=OE+OF=(3
+3)cm
②如图2,EF=OE-OF=(3
-3)cm,
故答案为:(3
+3)cm或(3
-3)cm.
①
 如图1,过O作OE⊥CD于E,延长EO交AB于F,
如图1,过O作OE⊥CD于E,延长EO交AB于F,∵AB∥CD,
∴EF⊥AB,
∵CO=DO=6cm,∠COD=60°,
∴CE=DE=3cm,∠OE⊥CD,
∴在Rt△CEO中,由勾股定理得:EO=
| 62-32 |
| 3 |
∵AO=BO,∠AOB=120°,EF⊥AB,
 ∴∠A=∠B=30°,∠AFO=90°,
∴∠A=∠B=30°,∠AFO=90°,∴OF=
| 1 |
| 2 |
∴EF=OE+OF=(3
| 3 |
②如图2,EF=OE-OF=(3
| 3 |
故答案为:(3
| 3 |
| 3 |
点评:本题考查了等腰三角形性质,三角形的内角和定理,勾股定理,等边三角形的性质,垂径定理的应用,主要考查学生的推理和计算能力,用了分类讨论思想.

练习册系列答案
相关题目
 4、如图,在10×10的正方形网格纸中,线段AB,CD的长均等于5.则图中到AB和CD所在直线的距离相等的网格点的个数有( )
4、如图,在10×10的正方形网格纸中,线段AB,CD的长均等于5.则图中到AB和CD所在直线的距离相等的网格点的个数有( ) (2013•金平区模拟)木工师傅在做完门框后,为防止变形常常像图中所示那样钉上两条斜拉的木板条(即图中的AB和CD),这样做的根据是( )
(2013•金平区模拟)木工师傅在做完门框后,为防止变形常常像图中所示那样钉上两条斜拉的木板条(即图中的AB和CD),这样做的根据是( ) (2013•松北区二模)如图,在半径为R的⊙O中,
(2013•松北区二模)如图,在半径为R的⊙O中,