题目内容
已知直角三角形x,y两边的长满足|x2-4|+
=0,则第三边长为( )
| y2-5y+6 |
分析:考查了非负数的性质,即若几个非负数的和为零,则每个非负数都为零,即可得到方程组,解方程组即可求得直角三角形的两边长,此时还要注意此两边可能都是直角边,也可能一个是直角边一个是斜边,注意别漏解.
解答:解:∵x,y两边的长满足|x2-4|+
=0,
∴x2-4=0且y2-5y+6=0,
∴x=±2,y1=2,y2=3,
∵x,y是三角形的边长,
∴x=2,y1=2,y2=3.
(1)当x=2,y=2是两直角边时,斜边长
=2
;
(2)当x=2,y=3是两直角边时,斜边长
=
;
(3)当x=2是直角边,y=3是斜边时,另一直角边长为
=
;
故选D.
| y2-5y+6 |
∴x2-4=0且y2-5y+6=0,
∴x=±2,y1=2,y2=3,
∵x,y是三角形的边长,
∴x=2,y1=2,y2=3.
(1)当x=2,y=2是两直角边时,斜边长
| 22+22 |
| 2 |
(2)当x=2,y=3是两直角边时,斜边长
| 22+32 |
| 13 |
(3)当x=2是直角边,y=3是斜边时,另一直角边长为
| 32-22 |
| 5 |
故选D.
点评:本题考查了非负数的和为零时,每个非负数为0,又考查了直接开方法,因式分解法以及勾股定理的运用,也考查了学生对所学知识的综合应用能力.

练习册系列答案
相关题目

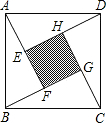 如图,是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.已知直角三角形的两个直角边长分别是1,2,小明随机地在大正方形及其内部区域投针,则针扎在小正方形区域的概率是
如图,是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.已知直角三角形的两个直角边长分别是1,2,小明随机地在大正方形及其内部区域投针,则针扎在小正方形区域的概率是