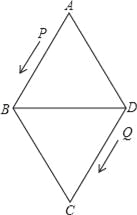
��Ŀ����
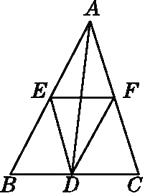
����Ŀ����ͼ������ABCD�ı߳�Ϊ24���ף���A=60������P�ӵ�A��������·AB��BD�������˶�����Q�ӵ�Dͬʱ��������·DC��CB��BA�������˶���
��1����BD�ij���
��2����֪��P��Q�˶����ٶȷֱ�Ϊ4����/�룬5����/�룬����12���P��Q�ֱ�M��N���㣬�����ǵĴ�С���з��࣬����ȷ����AMN����һ�������Σ���˵�����ɣ�
��3���裨2���еĵ�P��Q�ֱ��M��Nͬʱ��ԭ·���أ���P���ٶȲ��䣬��Q���ٶȸı�Ϊa����/�룬����3���P��Q�ֱ�E��F���㣬����BEF�루2���е���AMN���ƣ�����a��ֵ��
���𰸡���1��BD=24��2����AMN��ֱ�������Σ�3��2��6��12
�������������������1���������ε�����֤��ABD�ǵȱ������μ��ɣ�
��2�����P Q�ߵľ��룬�ٸ��ݵ������������ʼ����Ƴ��𰸣�
��3����Ϊ����������������ƣ��õ�����ʽ�����Q�ߵľ��룬��������𰸣�
�����������1��������ABCD��
��AB=AD��
�ߡ�A=60����
���ABD�ǵȱ������Σ�
��BD=AB=24���ף�
��BD=24���ף�
��2��12��ʱ��P����4��12=48��
��AB+BD=24+24=48��
��P��D�㣬
ͬ��Q��AB���е��ϣ�
��AD=BD��
��MN��AB��
���AMN��ֱ�������Σ�
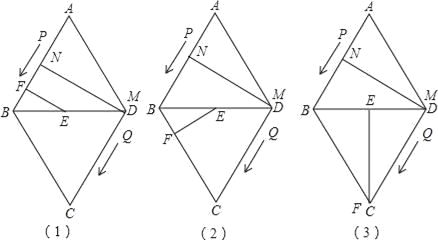
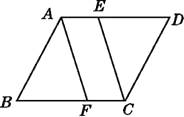
��3���������������ͼ��2��
��ANM=��EFB=90������A=��DBF=60����DE=3��4=12=![]() AD��
AD��
�����������������ʵã�BF=![]() AN=6��
AN=6��
��NB+BF=12+6=18��
��a=18��3=6��
ͬ������ͼ��1�����a=2��
��ͼ��3��a=12��
��a��ֵ��2��6��12��

 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�